Inverse Kinematics and Dexterous Workspace Formulation for 2-Segment Continuum Robots with Inextensible Segments
Paper and Code
Oct 05, 2021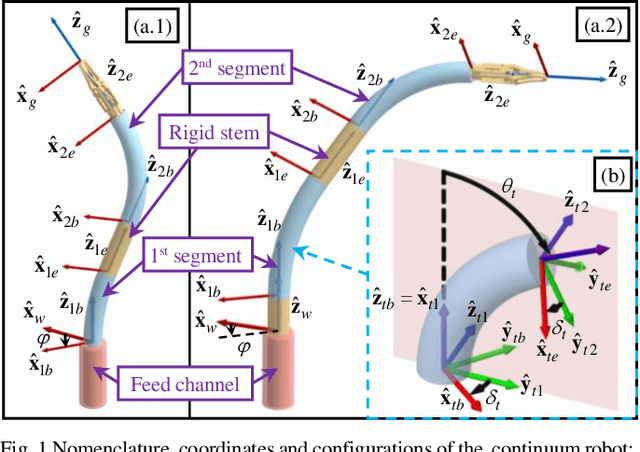
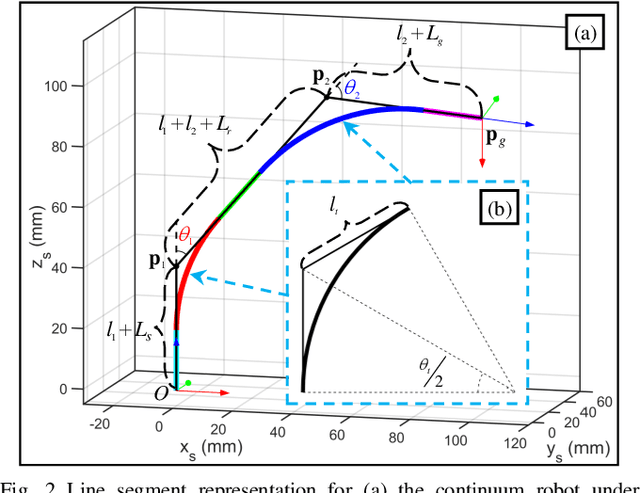
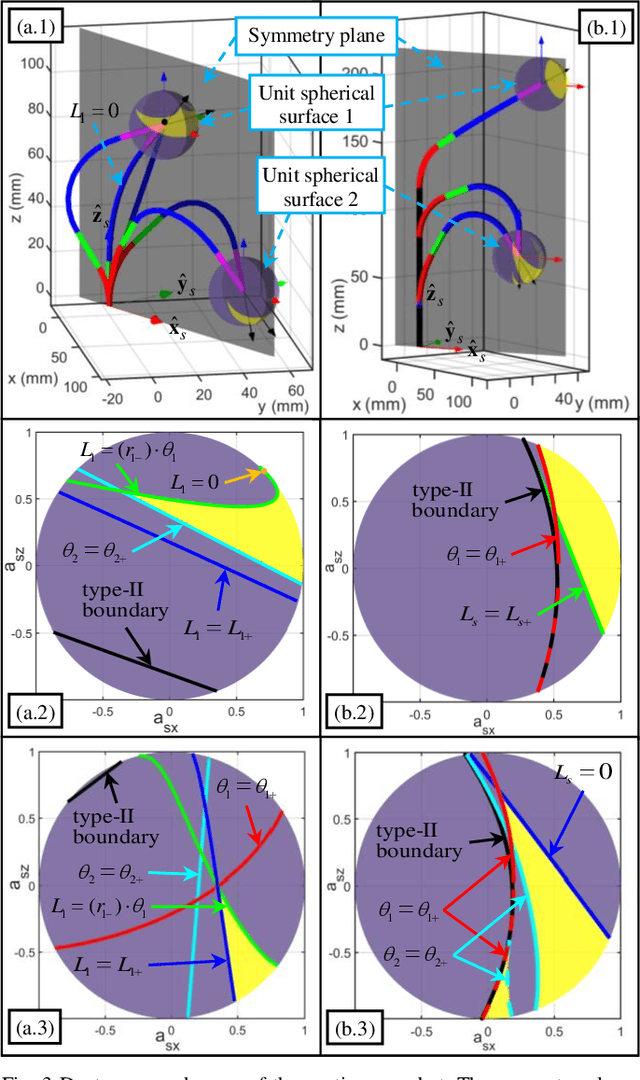
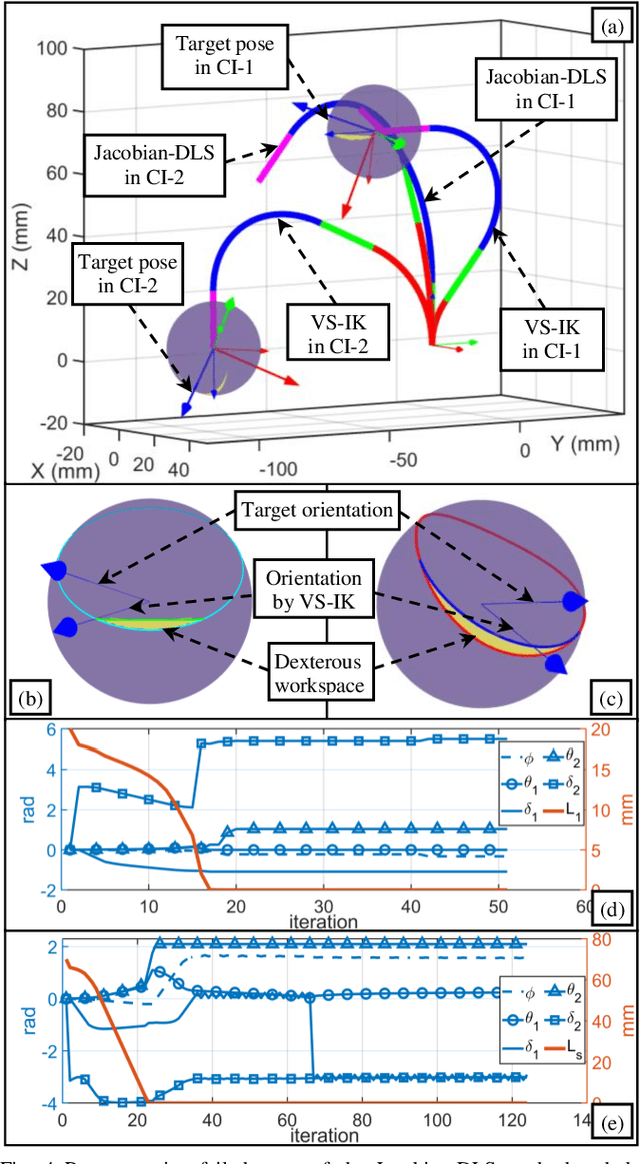
The inverse kinematics (IK) problem of continuum robots has been investigated in depth in the past decades. Under the constant-curvature bending assumption, closed-form IK solution has been obtained for continuum robots with variable segment lengths. Attempting to close the gap towards a complete solution, this paper presents an efficient solution for the IK problem of 2-segment continuum robots with one or two inextensible segments (a.k.a, constant segment lengths). Via representing the robot's shape as piecewise line segments, the configuration variables are separated from the IK formulation such that solving a one-variable nonlinear equation leads to the solution of the entire IK problem. Furthermore, an in-depth investigation of the boundaries of the dexterous workspace of the end effector caused by the configuration variables limits as well as the angular velocity singularities of the continuum robots was established. This dexterous workspace formulation, which is derived for the first time to the best of the authors' knowledge, is particularly useful to find the closest orientation to a target pose when the target orientation is out of the dexterous workspace. In the comparative simulation studies between the proposed method and the Jacobian-based IK method involving 500,000 cases, the proposed variable separation method solved 100% of the IK problems with much higher computational efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge