Interval Bound Propagation$\unicode{x2013}$aided Few$\unicode{x002d}$shot Learning

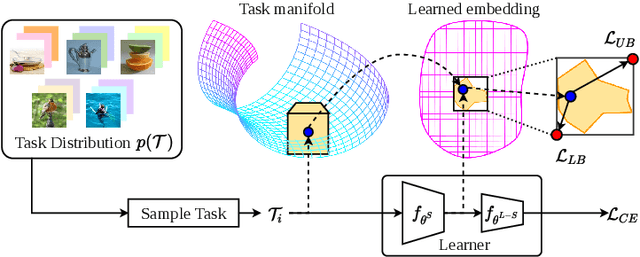
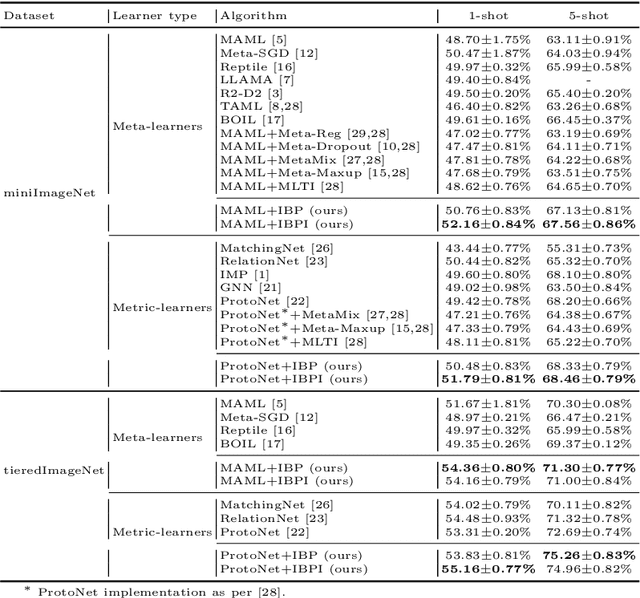
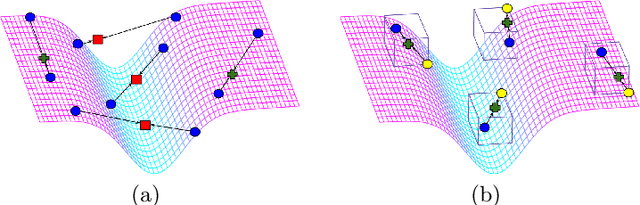
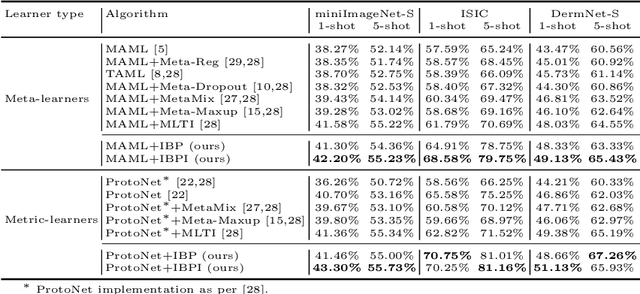
Few-shot learning aims to transfer the knowledge acquired from training on a diverse set of tasks, from a given task distribution, to generalize to unseen tasks, from the same distribution, with a limited amount of labeled data. The underlying requirement for effective few-shot generalization is to learn a good representation of the task manifold. One way to encourage this is to preserve local neighborhoods in the feature space learned by the few-shot learner. To this end, we introduce the notion of interval bounds from the provably robust training literature to few-shot learning. The interval bounds are used to characterize neighborhoods around the training tasks. These neighborhoods can then be preserved by minimizing the distance between a task and its respective bounds. We further introduce a novel strategy to artificially form new tasks for training by interpolating between the available tasks and their respective interval bounds, to aid in cases with a scarcity of tasks. We apply our framework to both model-agnostic meta-learning as well as prototype-based metric-learning paradigms. The efficacy of our proposed approach is evident from the improved performance on several datasets from diverse domains in comparison to a sizable number of recent competitors.