Interior Point Methods with Adversarial Networks
Paper and Code
May 23, 2018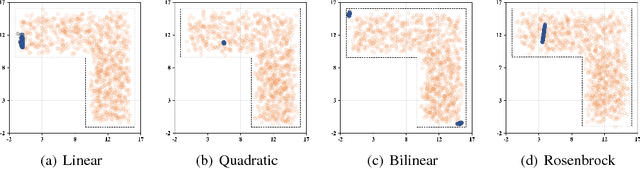


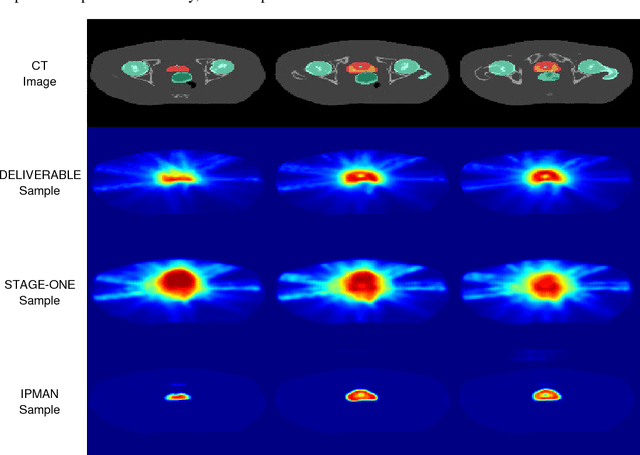
We present a new methodology, called IPMAN, that combines interior point methods and generative adversarial networks to solve constrained optimization problems with feasible sets that are non-convex or not explicitly defined. Our methodology produces {\epsilon}-optimal solutions and demonstrates that, when there are multiple global optima, it learns a distribution over the optimal set. We apply our approach to synthetic examples to demonstrate its effectiveness and to a problem in radiation therapy treatment optimization with a non-convex feasible set.
* 8 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge