Inter-layer Transition in Neural Architecture Search
Paper and Code
Nov 30, 2020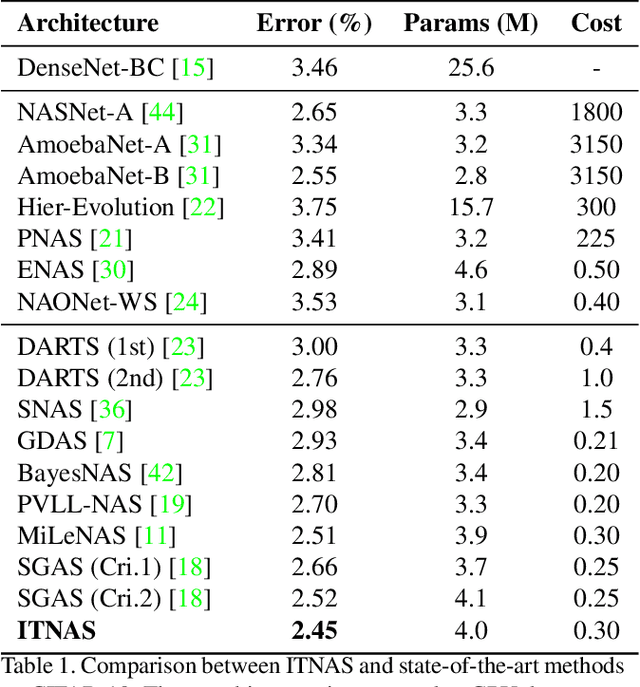
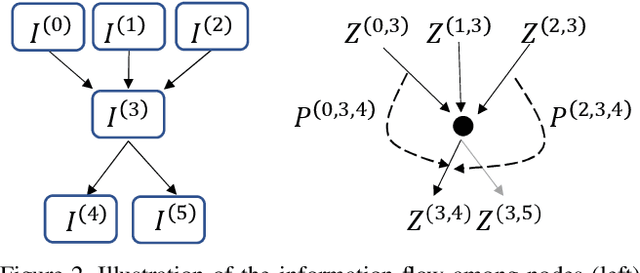

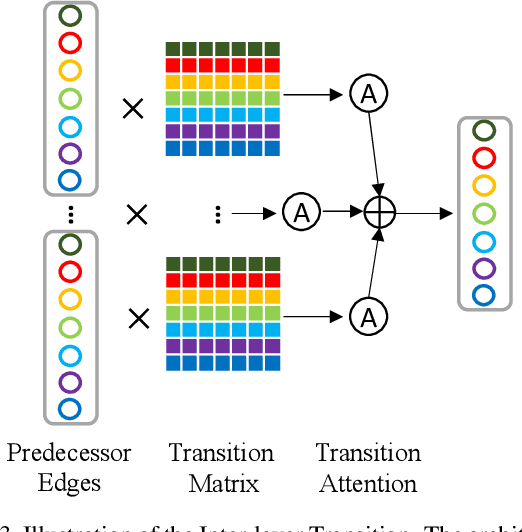
Differential Neural Architecture Search (NAS) methods represent the network architecture as a repetitive proxy directed acyclic graph (DAG) and optimize the network weights and architecture weights alternatively in a differential manner. However, existing methods model the architecture weights on each edge (i.e., a layer in the network) as statistically independent variables, ignoring the dependency between edges in DAG induced by their directed topological connections. In this paper, we make the first attempt to investigate such dependency by proposing a novel Inter-layer Transition NAS method. It casts the architecture optimization into a sequential decision process where the dependency between the architecture weights of connected edges is explicitly modeled. Specifically, edges are divided into inner and outer groups according to whether or not their predecessor edges are in the same cell. While the architecture weights of outer edges are optimized independently, those of inner edges are derived sequentially based on the architecture weights of their predecessor edges and the learnable transition matrices in an attentive probability transition manner. Experiments on five benchmarks confirm the value of modeling inter-layer dependency and demonstrate the proposed method outperforms state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge