Instance-Dependent PU Learning by Bayesian Optimal Relabeling
Paper and Code
Aug 07, 2018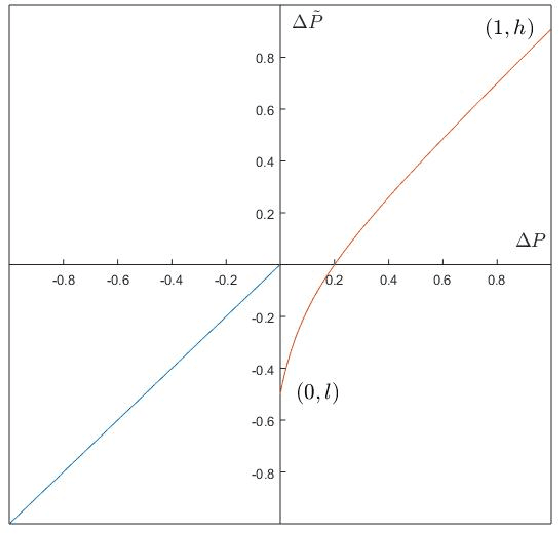
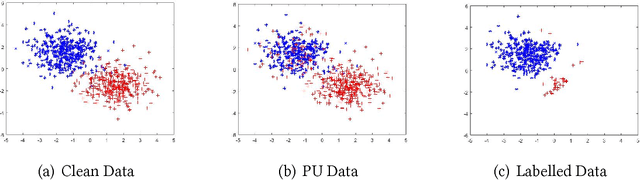
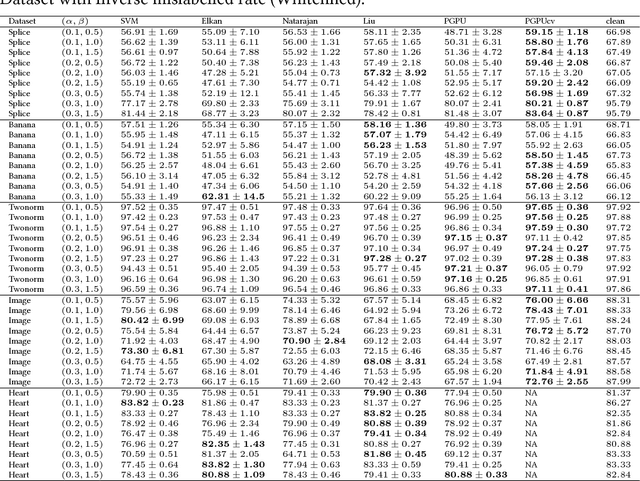

When learning from positive and unlabelled data, it is a strong assumption that the positive observations are randomly sampled from the distribution of $X$ conditional on $Y = 1$, where X stands for the feature and Y the label. Most existing algorithms are optimally designed under the assumption. However, for many real-world applications, the observed positive examples are dependent on the conditional probability $P(Y = 1|X)$ and should be sampled biasedly. In this paper, we assume that a positive example with a higher $P(Y = 1|X)$ is more likely to be labelled and propose a probabilistic-gap based PU learning algorithms. Specifically, by treating the unlabelled data as noisy negative examples, we could automatically label a group positive and negative examples whose labels are identical to the ones assigned by a Bayesian optimal classifier with a consistency guarantee. The relabelled examples have a biased domain, which is remedied by the kernel mean matching technique. The proposed algorithm is model-free and thus do not have any parameters to tune. Experimental results demonstrate that our method works well on both generated and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge