Input-agnostic Certified Group Fairness via Gaussian Parameter Smoothing
Paper and Code
Jun 22, 2022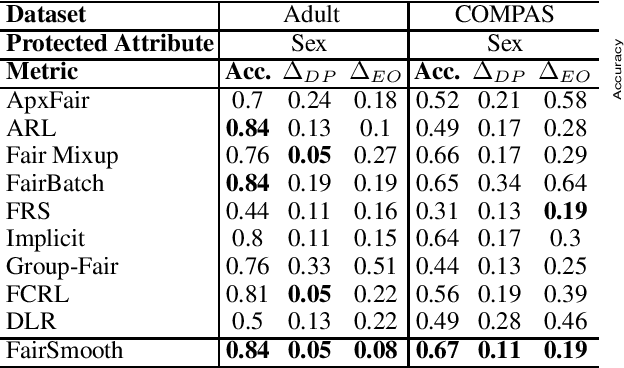
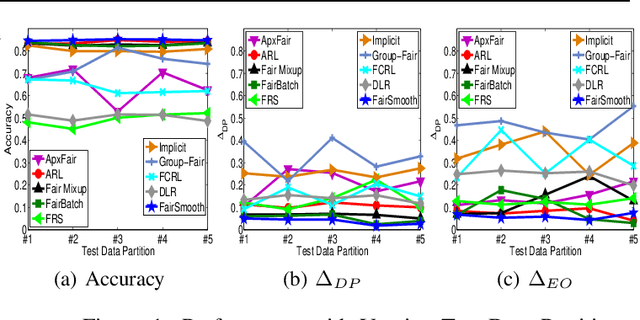
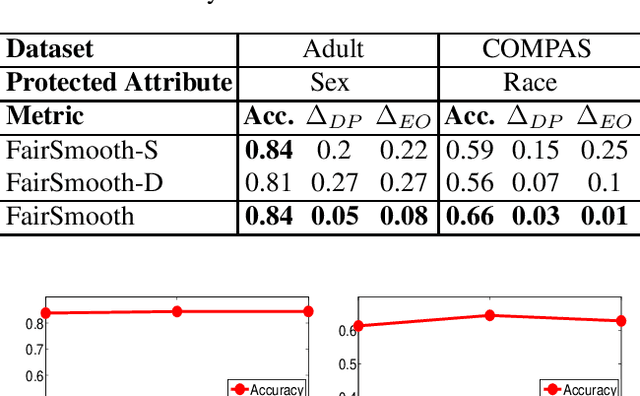
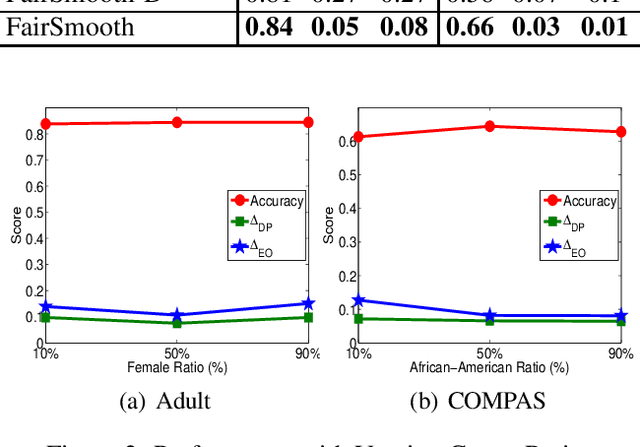
Only recently, researchers attempt to provide classification algorithms with provable group fairness guarantees. Most of these algorithms suffer from harassment caused by the requirement that the training and deployment data follow the same distribution. This paper proposes an input-agnostic certified group fairness algorithm, FairSmooth, for improving the fairness of classification models while maintaining the remarkable prediction accuracy. A Gaussian parameter smoothing method is developed to transform base classifiers into their smooth versions. An optimal individual smooth classifier is learnt for each group with only the data regarding the group and an overall smooth classifier for all groups is generated by averaging the parameters of all the individual smooth ones. By leveraging the theory of nonlinear functional analysis, the smooth classifiers are reformulated as output functions of a Nemytskii operator. Theoretical analysis is conducted to derive that the Nemytskii operator is smooth and induces a Frechet differentiable smooth manifold. We theoretically demonstrate that the smooth manifold has a global Lipschitz constant that is independent of the domain of the input data, which derives the input-agnostic certified group fairness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge