Information matrices and generalization

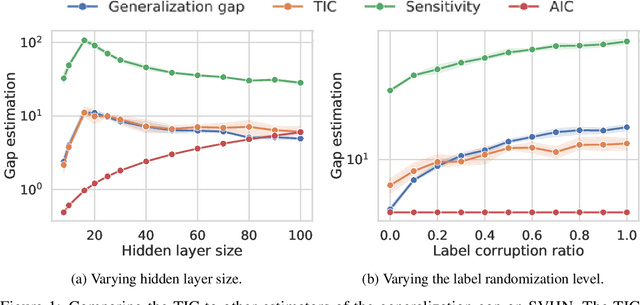
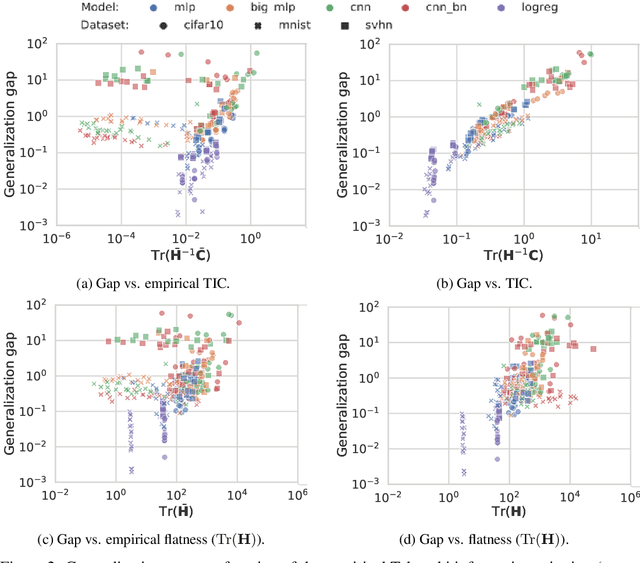
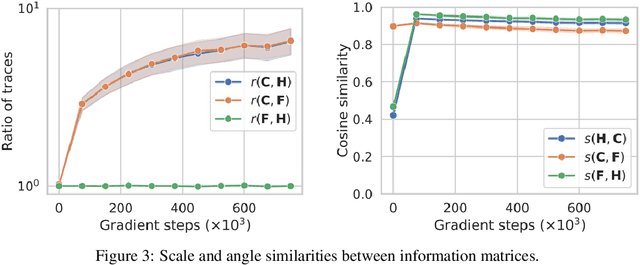
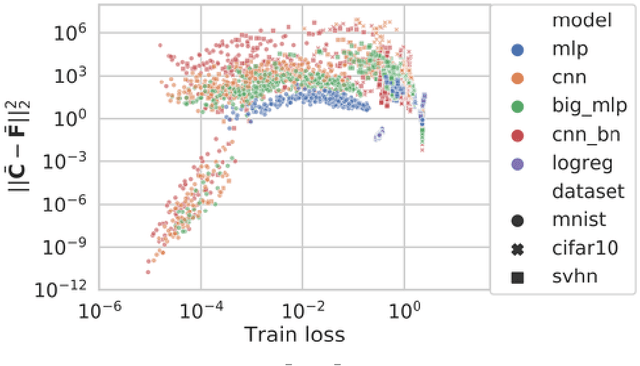
This work revisits the use of information criteria to characterize the generalization of deep learning models. In particular, we empirically demonstrate the effectiveness of the Takeuchi information criterion (TIC), an extension of the Akaike information criterion (AIC) for misspecified models, in estimating the generalization gap, shedding light on why quantities such as the number of parameters cannot quantify generalization. The TIC depends on both the Hessian of the loss H and the covariance of the gradients C. By exploring the similarities and differences between these two matrices as well as the Fisher information matrix F, we study the interplay between noise and curvature in deep models. We also address the question of whether C is a reasonable approximation to F, as is commonly assumed.