Inferring the quantum density matrix with machine learning
Paper and Code
Apr 11, 2019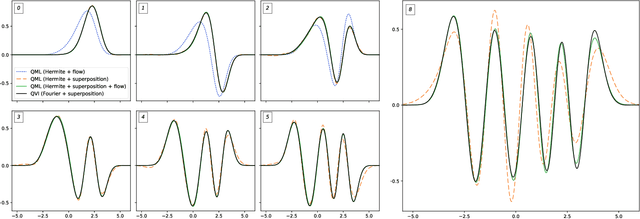

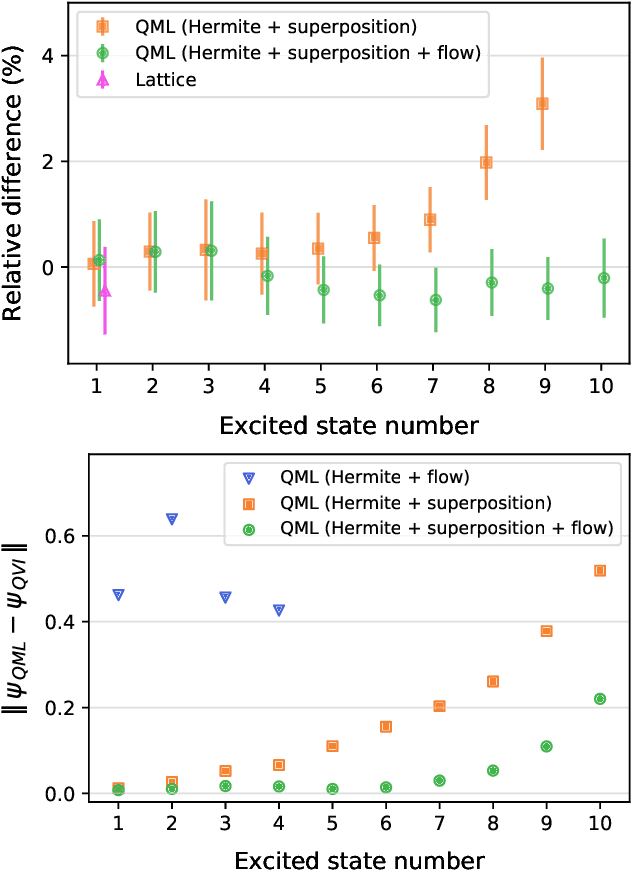

We introduce two methods for estimating the density matrix for a quantum system: Quantum Maximum Likelihood and Quantum Variational Inference. In these methods, we construct a variational family to model the density matrix of a mixed quantum state. We also introduce quantum flows, the quantum analog of normalizing flows, which can be used to increase the expressivity of this variational family. The eigenstates and eigenvalues of interest are then derived by optimizing an appropriate loss function. The approach is qualitatively different than traditional lattice techniques that rely on the time dependence of correlation functions that summarize the lattice configurations. The resulting estimate of the density matrix can then be used to evaluate the expectation of an arbitrary operator, which opens the door to new possibilities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge