Inferring Dynamic Bayesian Networks using Frequent Episode Mining
Paper and Code
Apr 14, 2009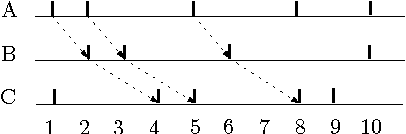
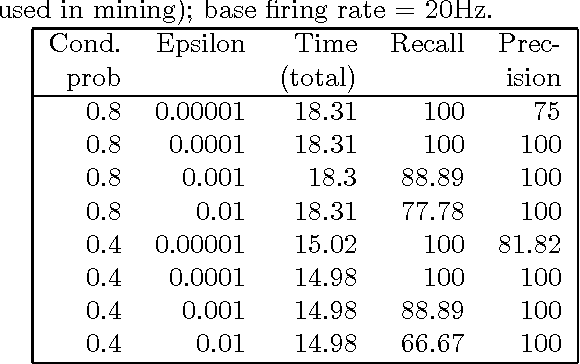
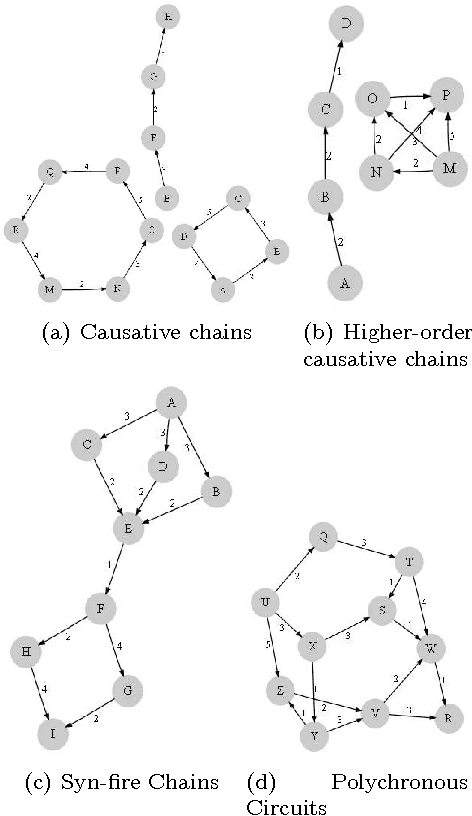
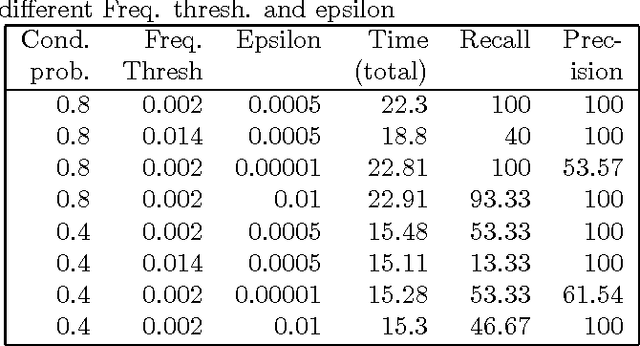
Motivation: Several different threads of research have been proposed for modeling and mining temporal data. On the one hand, approaches such as dynamic Bayesian networks (DBNs) provide a formal probabilistic basis to model relationships between time-indexed random variables but these models are intractable to learn in the general case. On the other, algorithms such as frequent episode mining are scalable to large datasets but do not exhibit the rigorous probabilistic interpretations that are the mainstay of the graphical models literature. Results: We present a unification of these two seemingly diverse threads of research, by demonstrating how dynamic (discrete) Bayesian networks can be inferred from the results of frequent episode mining. This helps bridge the modeling emphasis of the former with the counting emphasis of the latter. First, we show how, under reasonable assumptions on data characteristics and on influences of random variables, the optimal DBN structure can be computed using a greedy, local, algorithm. Next, we connect the optimality of the DBN structure with the notion of fixed-delay episodes and their counts of distinct occurrences. Finally, to demonstrate the practical feasibility of our approach, we focus on a specific (but broadly applicable) class of networks, called excitatory networks, and show how the search for the optimal DBN structure can be conducted using just information from frequent episodes. Application on datasets gathered from mathematical models of spiking neurons as well as real neuroscience datasets are presented. Availability: Algorithmic implementations, simulator codebases, and datasets are available from our website at http://neural-code.cs.vt.edu/dbn
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge