Inexact Simplification of Symbolic Regression Expressions with Locality-sensitive Hashing

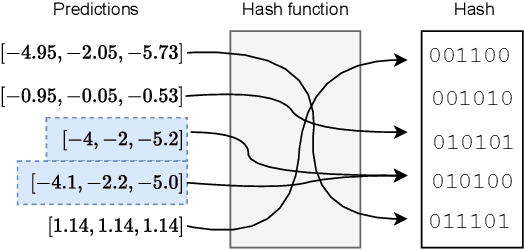
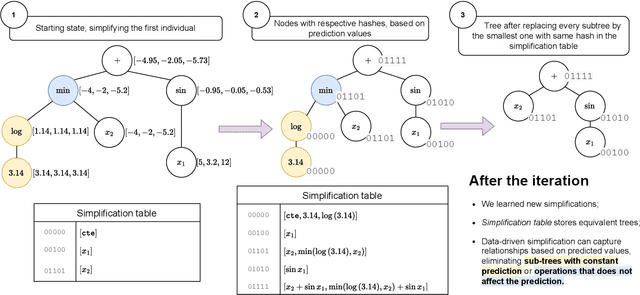
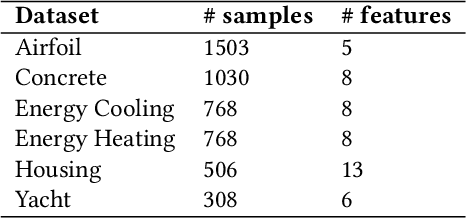
Symbolic regression (SR) searches for parametric models that accurately fit a dataset, prioritizing simplicity and interpretability. Despite this secondary objective, studies point out that the models are often overly complex due to redundant operations, introns, and bloat that arise during the iterative process, and can hinder the search with repeated exploration of bloated segments. Applying a fast heuristic algebraic simplification may not fully simplify the expression and exact methods can be infeasible depending on size or complexity of the expressions. We propose a novel agnostic simplification and bloat control for SR employing an efficient memoization with locality-sensitive hashing (LHS). The idea is that expressions and their sub-expressions traversed during the iterative simplification process are stored in a dictionary using LHS, enabling efficient retrieval of similar structures. We iterate through the expression, replacing subtrees with others of same hash if they result in a smaller expression. Empirical results shows that applying this simplification during evolution performs equal or better than without simplification in minimization of error, significantly reducing the number of nonlinear functions. This technique can learn simplification rules that work in general or for a specific problem, and improves convergence while reducing model complexity.