In Hindsight: A Smooth Reward for Steady Exploration
Paper and Code
Jun 24, 2019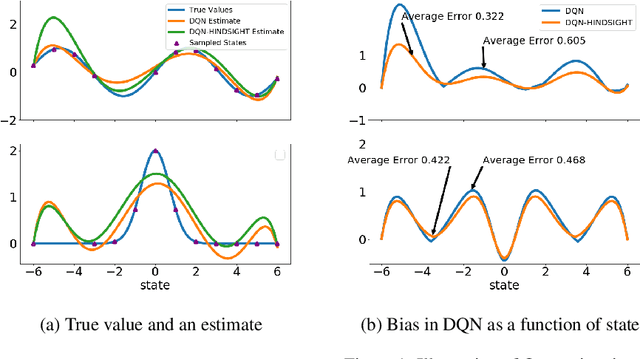
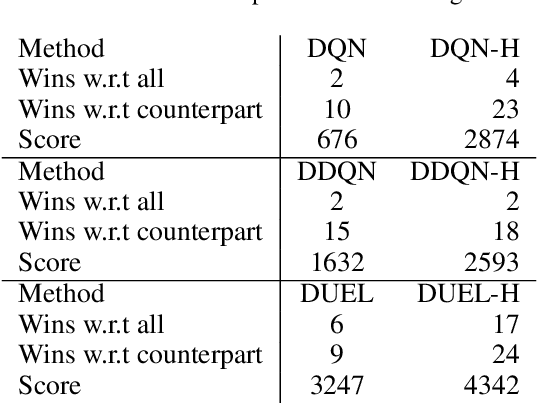
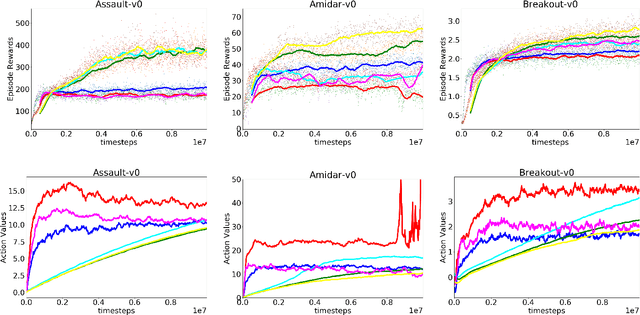
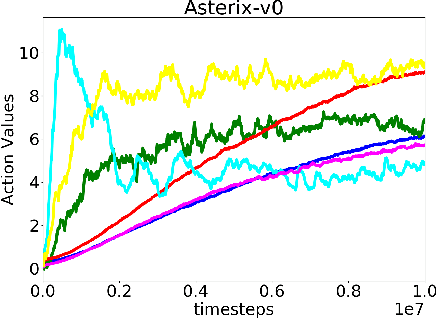
In classical Q-learning, the objective is to maximize the sum of discounted rewards through iteratively using the Bellman equation as an update, in an attempt to estimate the action value function of the optimal policy. Conventionally, the loss function is defined as the temporal difference between the action value and the expected (discounted) reward, however it focuses solely on the future, leading to overestimation errors. We extend the well-established Q-learning techniques by introducing the hindsight factor, an additional loss term that takes into account how the model progresses, by integrating the historic temporal difference as part of the reward. The effect of this modification is examined in a deterministic continuous-state space function estimation problem, where the overestimation phenomenon is significantly reduced and results in improved stability. The underlying effect of the hindsight factor is modeled as an adaptive learning rate, which unlike existing adaptive optimizers, takes into account the previously estimated action value. The proposed method outperforms variations of Q-learning, with an overall higher average reward and lower action values, which supports the deterministic evaluation, and proves that the hindsight factor contributes to lower overestimation errors. The mean average score of 100 episodes obtained after training for 10 million frames shows that the hindsight factor outperforms deep Q-networks, double deep Q-networks and dueling networks for a variety of ATARI games.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge