Improving the Performance of Stochastic Local Search for Maximum Vertex Weight Clique Problem Using Programming by Optimization
Paper and Code
Feb 27, 2020
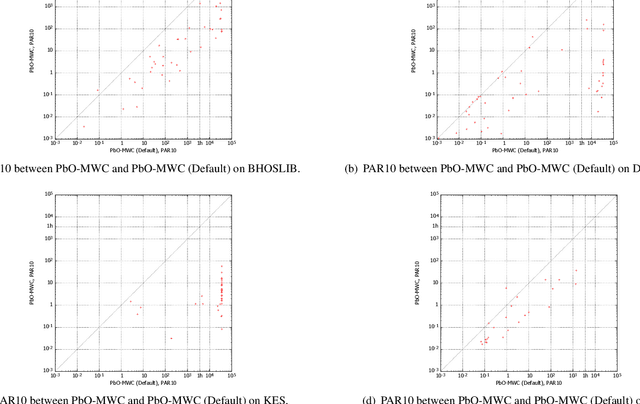


The maximum vertex weight clique problem (MVWCP) is an important generalization of the maximum clique problem (MCP) that has a wide range of real-world applications. In situations where rigorous guarantees regarding the optimality of solutions are not required, MVWCP is usually solved using stochastic local search (SLS) algorithms, which also define the state of the art for solving this problem. However, there is no single SLS algorithm which gives the best performance across all classes of MVWCP instances, and it is challenging to effectively identify the most suitable algorithm for each class of MVWCP instances. In this work, we follow the paradigm of Programming by Optimization (PbO) to develop a new, flexible and highly parametric SLS framework for solving MVWCP, combining, for the first time, a broad range of effective heuristic mechanisms. By automatically configuring this PbO-MWC framework, we achieve substantial advances in the state-of-the-art in solving MVWCP over a broad range of prominent benchmarks, including two derived from real-world applications in transplantation medicine (kidney exchange) and assessment of research excellence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge