Improving Screening Processes via Calibrated Subset Selection

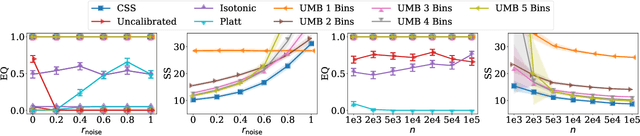
Many selection processes such as finding patients qualifying for a medical trial or retrieval pipelines in search engines consist of multiple stages, where an initial screening stage focuses the resources on shortlisting the most promising candidates. In this paper, we investigate what guarantees a screening classifier can provide, independently of whether it is constructed manually or trained. We find that current solutions do not enjoy distribution-free theoretical guarantees -- we show that, in general, even for a perfectly calibrated classifier, there always exist specific pools of candidates for which its shortlist is suboptimal. Then, we develop a distribution-free screening algorithm -- called Calibrated Subset Selection (CSS) -- that, given any classifier and some amount of calibration data, finds near-optimal shortlists of candidates that contain a desired number of qualified candidates in expectation. Moreover, we show that a variant of our algorithm that calibrates a given classifier multiple times across specific groups can create shortlists with provable diversity guarantees. Experiments on US Census survey data validate our theoretical results and show that the shortlists provided by our algorithm are superior to those provided by several competitive baselines.