Improving Policy-Constrained Kidney Exchange via Pre-Screening
Paper and Code
Oct 22, 2020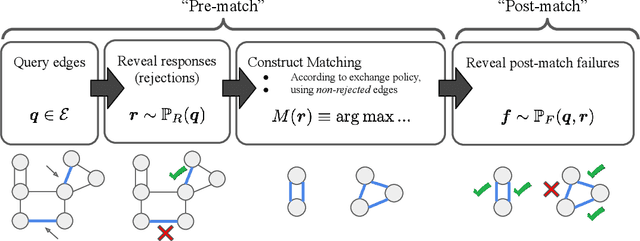
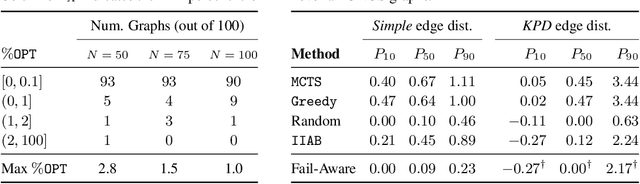
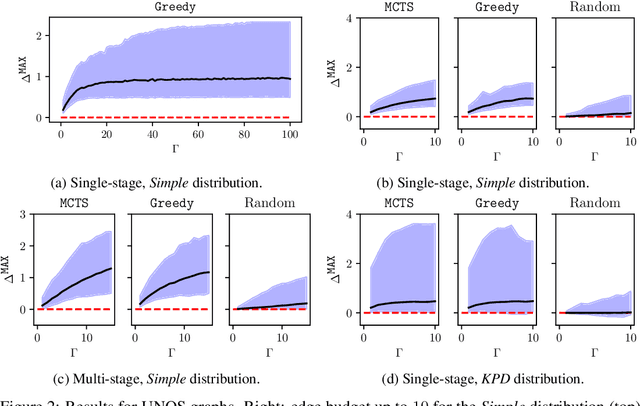
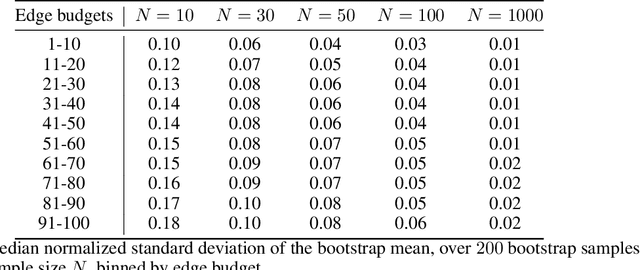
In barter exchanges, participants swap goods with one another without exchanging money; exchanges are often facilitated by a central clearinghouse, with the goal of maximizing the aggregate quality (or number) of swaps. Barter exchanges are subject to many forms of uncertainty--in participant preferences, the feasibility and quality of various swaps, and so on. Our work is motivated by kidney exchange, a real-world barter market in which patients in need of a kidney transplant swap their willing living donors, in order to find a better match. Modern exchanges include 2- and 3-way swaps, making the kidney exchange clearing problem NP-hard. Planned transplants often fail for a variety of reasons--if the donor organ is refused by the recipient's medical team, or if the donor and recipient are found to be medically incompatible. Due to 2- and 3-way swaps, failed transplants can "cascade" through an exchange; one US-based exchange estimated that about 85% of planned transplants failed in 2019. Many optimization-based approaches have been designed to avoid these failures; however most exchanges cannot implement these methods due to legal and policy constraints. Instead we consider a setting where exchanges can query the preferences of certain donors and recipients--asking whether they would accept a particular transplant. We characterize this as a two-stage decision problem, in which the exchange program (a) queries a small number of transplants before committing to a matching, and (b) constructs a matching according to fixed policy. We show that selecting these edges is a challenging combinatorial problem, which is non-monotonic and non-submodular, in addition to being NP-hard. We propose both a greedy heuristic and a Monte Carlo tree search, which outperforms previous approaches, using experiments on both synthetic data and real kidney exchange data from the United Network for Organ Sharing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge