Improving Convolutional Neural Networks Via Conservative Field Regularisation and Integration
Paper and Code
Mar 11, 2020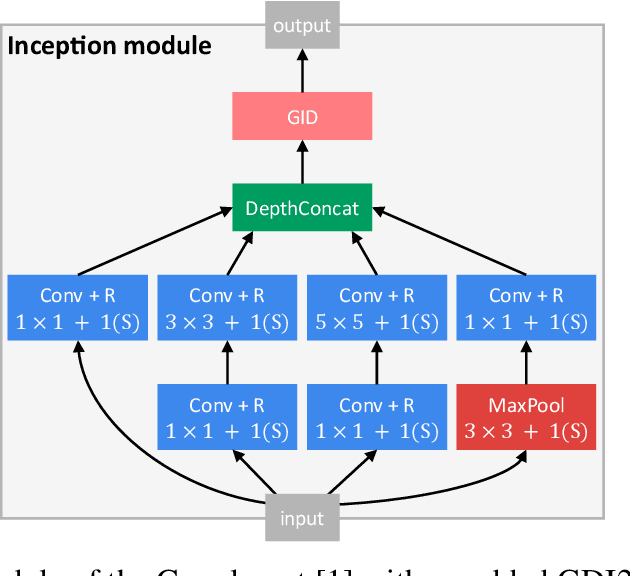
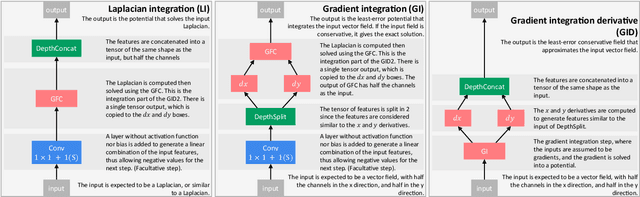
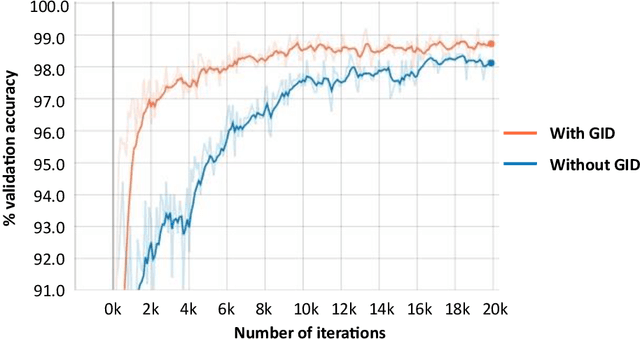
Current research in convolutional neural networks (CNN) focuses mainly on changing the architecture of the networks, optimizing the hyper-parameters and improving the gradient descent. However, most work use only 3 standard families of operations inside the CNN, the convolution, the activation function, and the pooling. In this work, we propose a new family of operations based on the Green's function of the Laplacian, which allows the network to solve the Laplacian, to integrate any vector field and to regularize the field by forcing it to be conservative. Hence, the Green's function (GF) is the first operation that regularizes the 2D or 3D feature space by forcing it to be conservative and physically interpretable, instead of regularizing the norm of the weights. Our results show that such regularization allows the network to learn faster, to have smoother training curves and to better generalize, without any additional parameter. The current manuscript presents early results, more work is required to benchmark the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge