Imposing Exact Safety Specifications in Neural Reachable Tubes
Paper and Code
Mar 31, 2024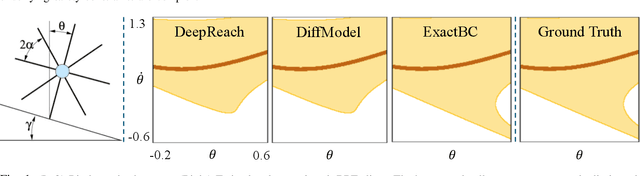
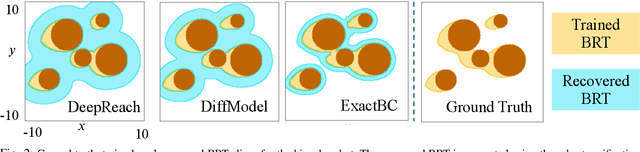
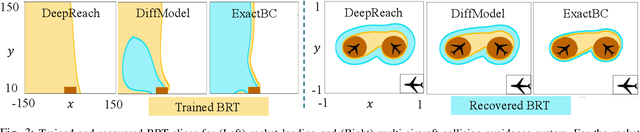

Hamilton-Jacobi (HJ) reachability analysis is a verification tool that provides safety and performance guarantees for autonomous systems. It is widely adopted because of its ability to handle nonlinear dynamical systems with bounded adversarial disturbances and constraints on states and inputs. However, it involves solving a PDE to compute a safety value function, whose computational and memory complexity scales exponentially with the state dimension, making its direct usage in large-scale systems intractable. Recently, a learning-based approach called DeepReach, has been proposed to approximate high-dimensional reachable tubes using neural networks. While DeepReach has been shown to be effective, the accuracy of the learned solution decreases with the increase in system complexity. One of the reasons for this degradation is the inexact imposition of safety constraints during the learning process, which corresponds to the PDE's boundary conditions. Specifically, DeepReach imposes boundary conditions as soft constraints in the loss function, which leaves room for error during the value function learning. Moreover, one needs to carefully adjust the relative contributions from the imposition of boundary conditions and the imposition of the PDE in the loss function. This, in turn, induces errors in the overall learned solution. In this work, we propose a variant of DeepReach that exactly imposes safety constraints during the learning process by restructuring the overall value function as a weighted sum of the boundary condition and neural network output. This eliminates the need for a boundary loss during training, thus bypassing the need for loss adjustment. We demonstrate the efficacy of the proposed approach in significantly improving the accuracy of learned solutions for challenging high-dimensional reachability tasks, such as rocket-landing and multivehicle collision-avoidance problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge