Image Fusion via Sparse Regularization with Non-Convex Penalties

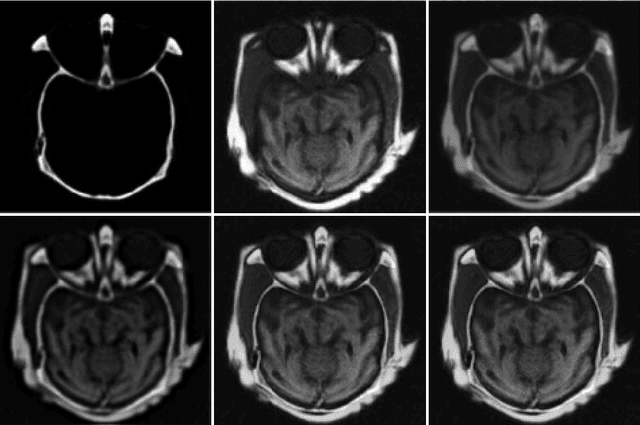
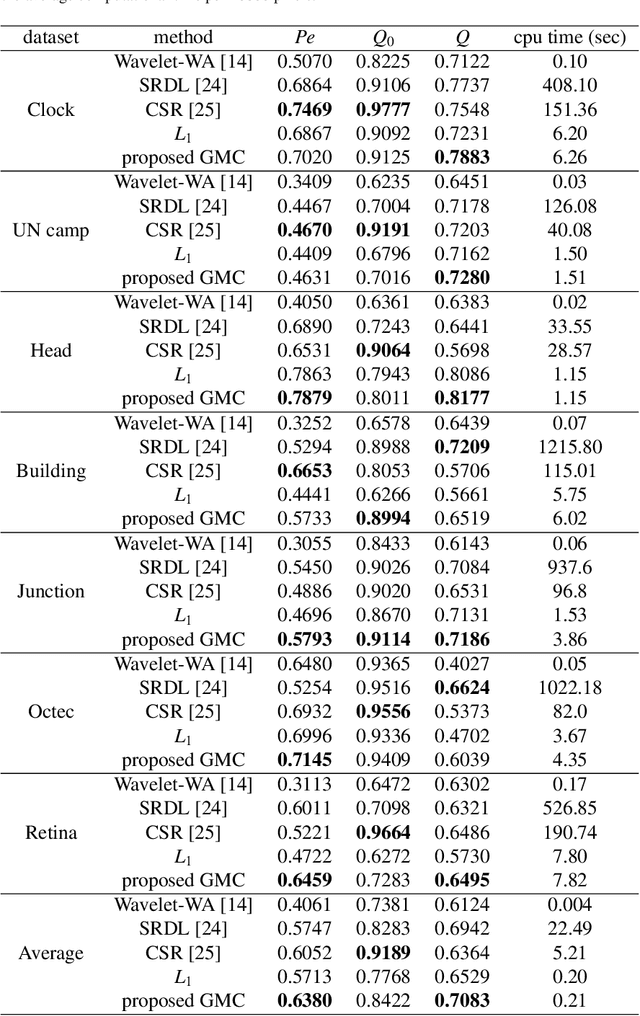
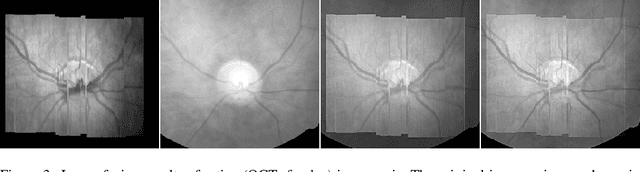
The L1 norm regularized least squares method is often used for finding sparse approximate solutions and is widely used in 1-D signal restoration. Basis pursuit denoising (BPD) performs noise reduction in this way. However, the shortcoming of using L1 norm regularization is the underestimation of the true solution. Recently, a class of non-convex penalties have been proposed to improve this situation. This kind of penalty function is non-convex itself, but preserves the convexity property of the whole cost function. This approach has been confirmed to offer good performance in 1-D signal denoising. This paper demonstrates the aforementioned method to 2-D signals (images) and applies it to multisensor image fusion. The problem is posed as an inverse one and a corresponding cost function is judiciously designed to include two data attachment terms. The whole cost function is proved to be convex upon suitably choosing the non-convex penalty, so that the cost function minimization can be tackled by convex optimization approaches, which comprise simple computations. The performance of the proposed method is benchmarked against a number of state-of-the-art image fusion techniques and superior performance is demonstrated both visually and in terms of various assessment measures.