Image Denoising Using Sparsifying Transform Learning and Weighted Singular Values Minimization
Paper and Code
Apr 02, 2020
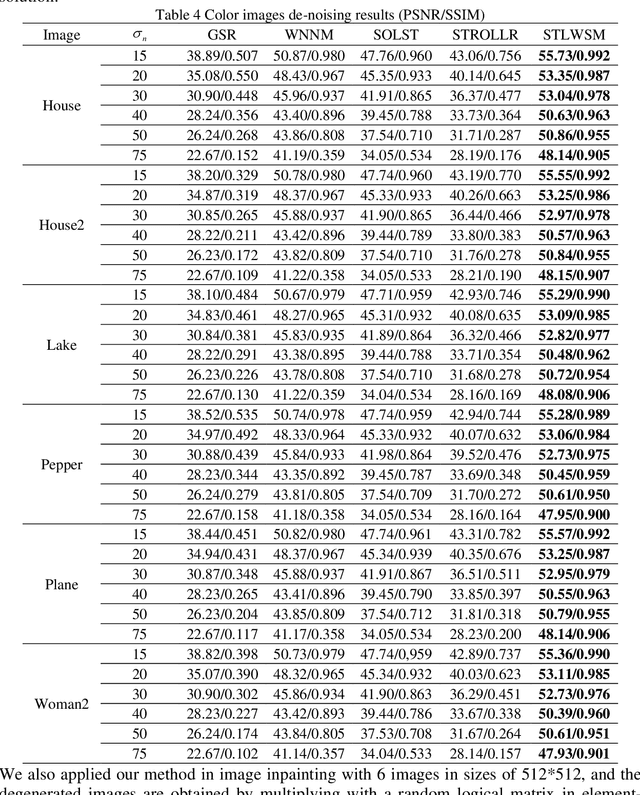
In image denoising (IDN) processing, the low-rank property is usually considered as an important image prior. As a convex relaxation approximation of low rank, nuclear norm based algorithms and their variants have attracted significant attention. These algorithms can be collectively called image domain based methods, whose common drawback is the requirement of great number of iterations for some acceptable solution. Meanwhile, the sparsity of images in a certain transform domain has also been exploited in image denoising problems. Sparsity transform learning algorithms can achieve extremely fast computations as well as desirable performance. By taking both advantages of image domain and transform domain in a general framework, we propose a sparsity transform learning and weighted singular values minimization method (STLWSM) for IDN problems. The proposed method can make full use of the preponderance of both domains. For solving the non-convex cost function, we also present an efficient alternative solution for acceleration. Experimental results show that the proposed STLWSM achieves improvement both visually and quantitatively with a large margin over state-of-the-art approaches based on an alternatively single domain. It also needs much less iteration than all the image domain algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge