Hyperbolic Hierarchical Knowledge Graph Embeddings for Link Prediction in Low Dimensions

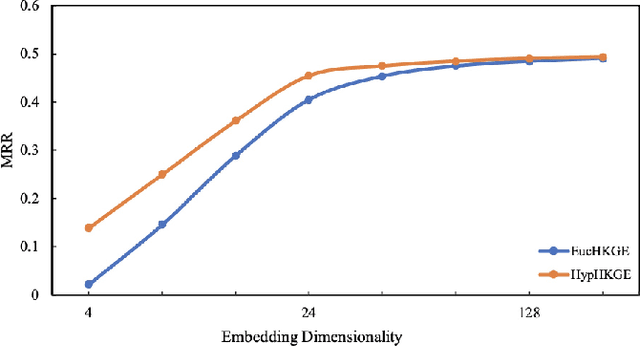
Knowledge graph embeddings (KGE) have been validated as powerful methods for inferring missing links in knowledge graphs (KGs) since they map entities into Euclidean space and treat relations as transformations of entities. Currently, some Euclidean KGE methods model semantic hierarchies prevalent in KGs and promote the performance of link prediction. For hierarchical data, instead of traditional Euclidean space, hyperbolic space as an embedding space has shown the promise of high fidelity and low memory consumption; however, existing hyperbolic KGE methods neglect to model them. To address this issue, we propose a novel KGE model -- hyperbolic hierarchical KGE (HypHKGE). To be specific, we first design the attention-based learnable curvatures for hyperbolic space to preserve rich semantic hierarchies. Moreover, we define the hyperbolic hierarchical transformations based on the theory of hyperbolic geometry, which utilize hierarchies that we preserved to infer the links. Experiments show that HypHKGE can effectively model semantic hierarchies in hyperbolic space and outperforms the state-of-the-art hyperbolic methods, especially in low dimensions.