Hyperbolic Geometry in Computer Vision: A Survey
Paper and Code
Apr 21, 2023


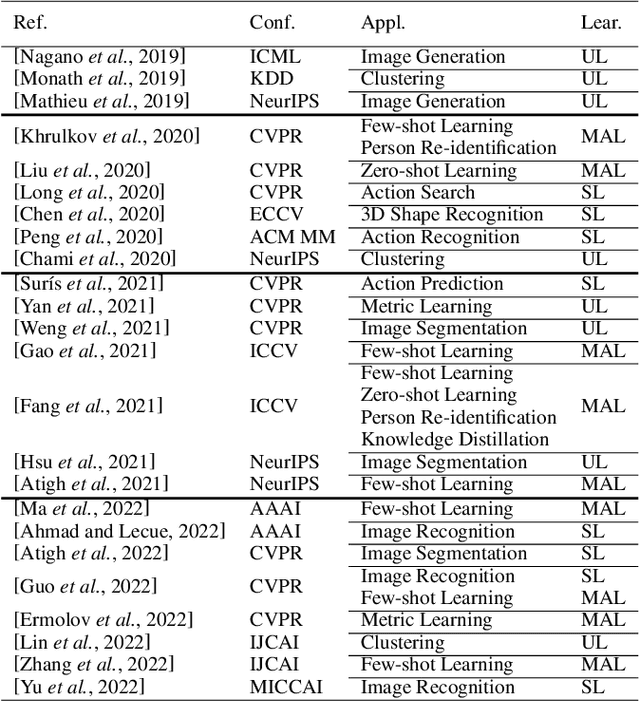
Hyperbolic geometry, a Riemannian manifold endowed with constant sectional negative curvature, has been considered an alternative embedding space in many learning scenarios, \eg, natural language processing, graph learning, \etc, as a result of its intriguing property of encoding the data's hierarchical structure (like irregular graph or tree-likeness data). Recent studies prove that such data hierarchy also exists in the visual dataset, and investigate the successful practice of hyperbolic geometry in the computer vision (CV) regime, ranging from the classical image classification to advanced model adaptation learning. This paper presents the first and most up-to-date literature review of hyperbolic spaces for CV applications. To this end, we first introduce the background of hyperbolic geometry, followed by a comprehensive investigation of algorithms, with geometric prior of hyperbolic space, in the context of visual applications. We also conclude this manuscript and identify possible future directions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge