How Powerful is Graph Filtering for Recommendation
Paper and Code
Jun 13, 2024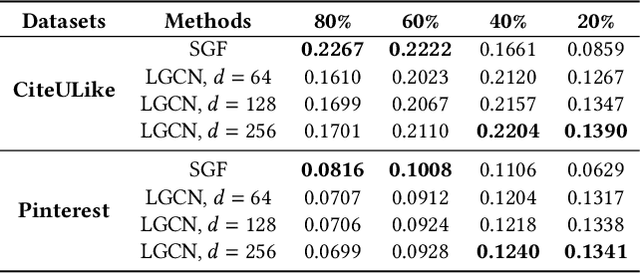
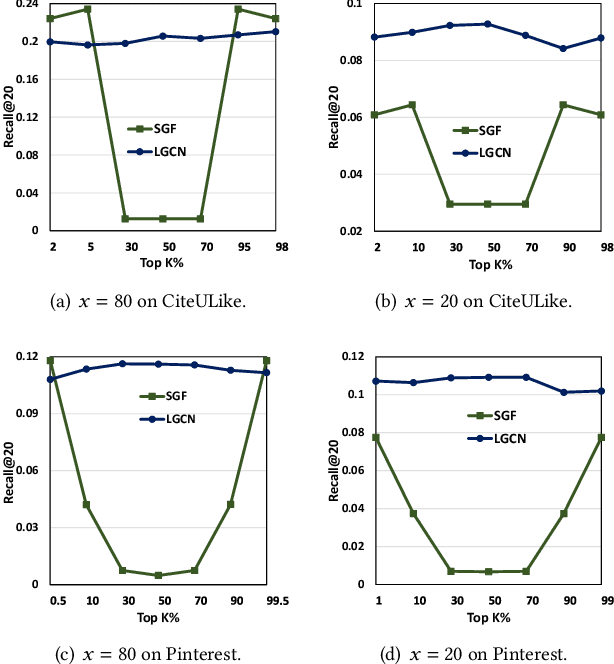
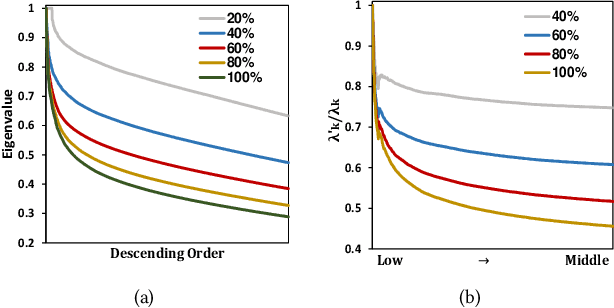
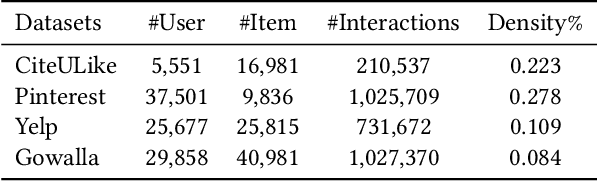
It has been shown that the effectiveness of graph convolutional network (GCN) for recommendation is attributed to the spectral graph filtering. Most GCN-based methods consist of a graph filter or followed by a low-rank mapping optimized based on supervised training. However, we show two limitations suppressing the power of graph filtering: (1) Lack of generality. Due to the varied noise distribution, graph filters fail to denoise sparse data where noise is scattered across all frequencies, while supervised training results in worse performance on dense data where noise is concentrated in middle frequencies that can be removed by graph filters without training. (2) Lack of expressive power. We theoretically show that linear GCN (LGCN) that is effective on collaborative filtering (CF) cannot generate arbitrary embeddings, implying the possibility that optimal data representation might be unreachable. To tackle the first limitation, we show close relation between noise distribution and the sharpness of spectrum where a sharper spectral distribution is more desirable causing data noise to be separable from important features without training. Based on this observation, we propose a generalized graph normalization G^2N to adjust the sharpness of spectral distribution in order to redistribute data noise to assure that it can be removed by graph filtering without training. As for the second limitation, we propose an individualized graph filter (IGF) adapting to the different confidence levels of the user preference that interactions can reflect, which is proved to be able to generate arbitrary embeddings. By simplifying LGCN, we further propose a simplified graph filtering (SGFCF) which only requires the top-K singular values for recommendation. Finally, experimental results on four datasets with different density settings demonstrate the effectiveness and efficiency of our proposed methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge