How Compact?: Assessing Compactness of Representations through Layer-Wise Pruning
Paper and Code
Jan 09, 2019
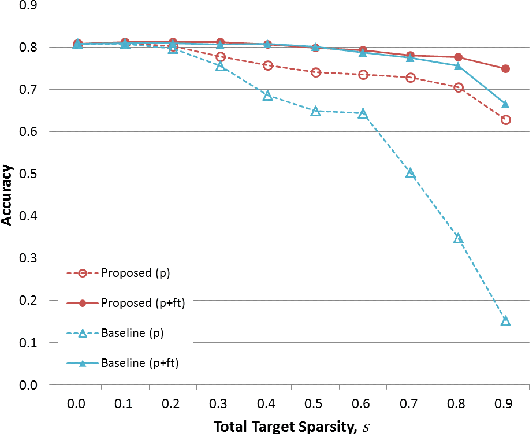
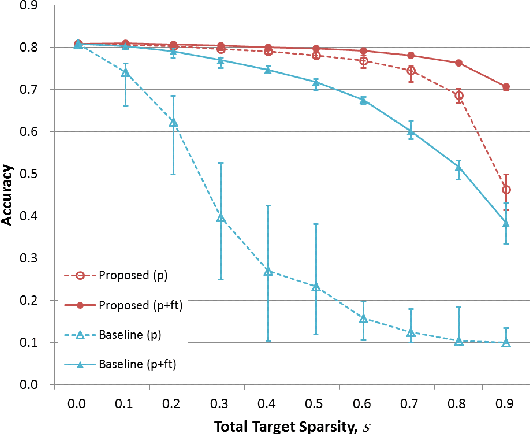
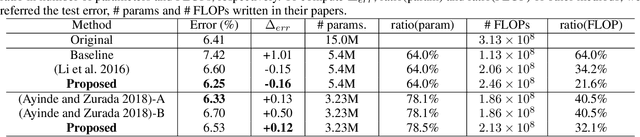
Various forms of representations may arise in the many layers embedded in deep neural networks (DNNs). Of these, where can we find the most compact representation? We propose to use a pruning framework to answer this question: How compact can each layer be compressed, without losing performance? Most of the existing DNN compression methods do not consider the relative compressibility of the individual layers. They uniformly apply a single target sparsity to all layers or adapt layer sparsity using heuristics and additional training. We propose a principled method that automatically determines the sparsity of individual layers derived from the importance of each layer. To do this, we consider a metric to measure the importance of each layer based on the layer-wise capacity. Given the trained model and the total target sparsity, we first evaluate the importance of each layer from the model. From the evaluated importance, we compute the layer-wise sparsity of each layer. The proposed method can be applied to any DNN architecture and can be combined with any pruning method that takes the total target sparsity as a parameter. To validate the proposed method, we carried out an image classification task with two types of DNN architectures on two benchmark datasets and used three pruning methods for compression. In case of VGG-16 model with weight pruning on the ImageNet dataset, we achieved up to 75% (17.5% on average) better top-5 accuracy than the baseline under the same total target sparsity. Furthermore, we analyzed where the maximum compression can occur in the network. This kind of analysis can help us identify the most compact representation within a deep neural network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge