How can a Cognitive Radar Mask its Cognition?
Paper and Code
Oct 16, 2021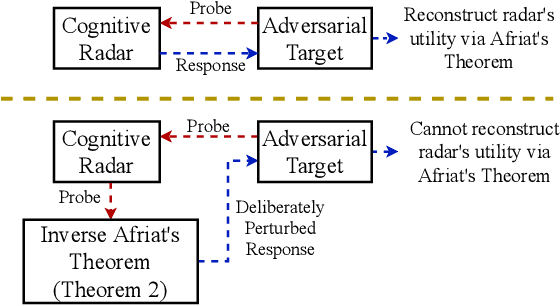
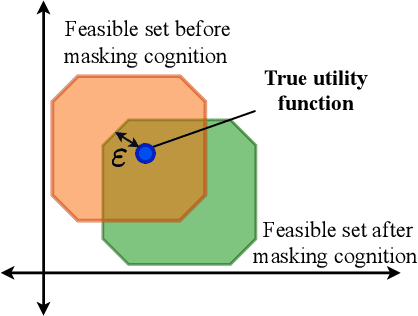
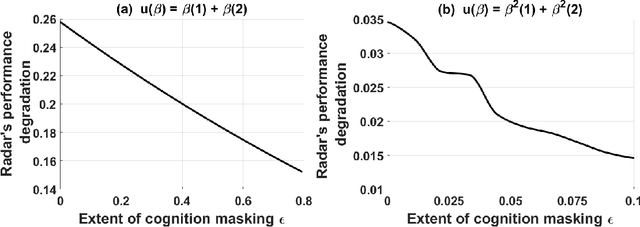
We study how a cognitive radar can mask (hide) its cognitive ability from an adversarial jamming device. Specifically, if the radar optimally adapts its waveform based on adversarial target maneuvers (probes), how should the radar choose its waveform parameters (response) so that its utility function cannot be recovered by the adversary. This paper abstracts the radar's cognition masking problem in terms of the spectra (eigenvalues) of the state and observation noise covariance matrices, and embeds the algebraic Riccati equation into an economics-based utility maximization setup. Given an observed sequence of radar responses, the adversary tests for utility maximization behavior of the radar and estimates its utility function that rationalizes the radar's responses. In turn, the radar deliberately chooses sub-optimal responses so that its utility function almost fails the utility maximization test, and hence, its cognitive ability is masked from the adversary. We illustrate the performance of our cognition masking scheme via simple numerical examples. Our approach in this paper is based on revealed preference theory in microeconomics for identifying rationality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge