Highway Traffic State Estimation Using Physics Regularized Gaussian Process: Discretized Formulation

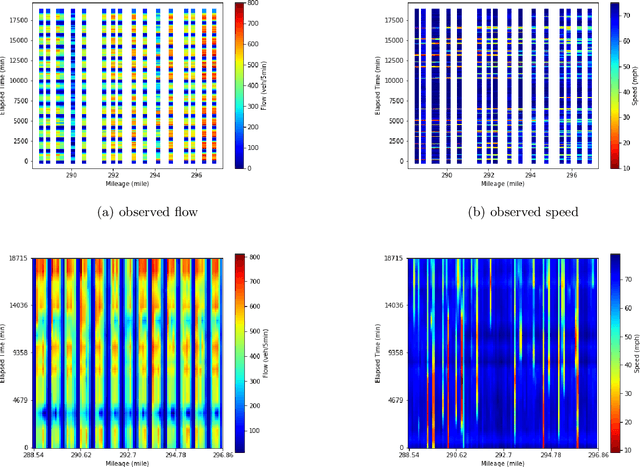
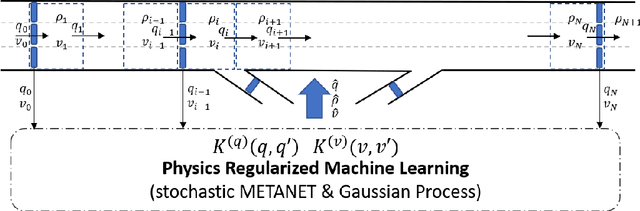
Despite the success of classical traffic flow (e.g., second-order macroscopic) models and data-driven (e.g., Machine Learning - ML) approaches in traffic state estimation, those approaches either require great efforts for parameter calibrations or lack theoretical interpretation. To fill this research gap, this study presents a new modeling framework, named physics regularized Gaussian process (PRGP). This novel approach can encode physics models, i.e., classical traffic flow models, into the Gaussian process architecture and so as to regularize the ML training process. Particularly, this study aims to discuss how to develop a PRGP model when the original physics model is with discrete formulations. Then based on the posterior regularization inference framework, an efficient stochastic optimization algorithm is developed to maximize the evidence lowerbound of the system likelihood. To prove the effectiveness of the proposed model, this paper conducts empirical studies on a real-world dataset that is collected from a stretch of I-15 freeway, Utah. Results show the new PRGP model can outperform the previous compatible methods, such as calibrated physics models and pure machine learning methods, in estimation precision and input robustness.