High-quality Ellipse Detection Based on Arc-support Line Segments

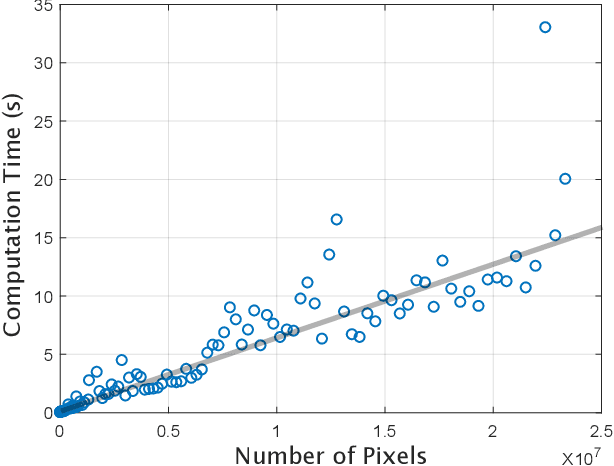
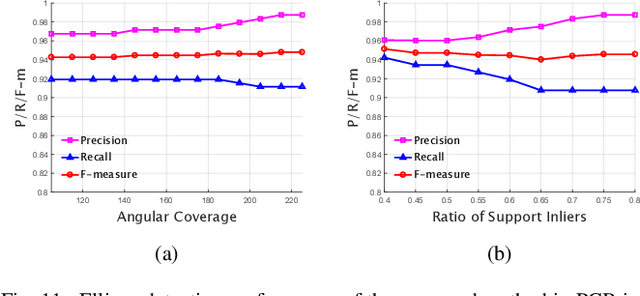
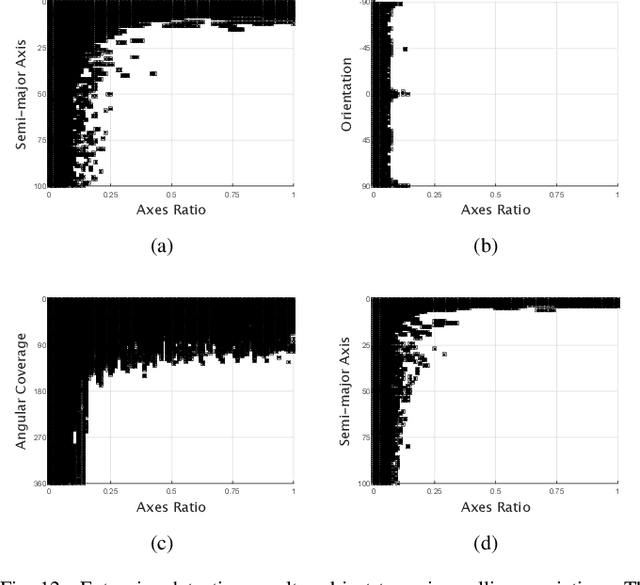
Over the years many ellipse detection algorithms spring up and are studied broadly, while the critical issue of detecting ellipses accurately and efficiently in real-world images remains a challenge. In this paper, an accurate and efficient ellipse detector by arc-support line segments is proposed. The arc-support line segment simplifies the complicated expression of curves in an image while retains the general properties including convexity and polarity, which grounds the successful detection of ellipses. The arc-support groups are formed by iteratively and robustly linking the arc-support line segments that latently belong to a common ellipse at point statistics level. Afterward, two complementary approaches, namely, selecting the group with higher saliency to fit an ellipse, and searching all the valid paired arc-support groups, are utilized to generate the initial ellipse set, both locally and globally. In ellipse fitting step, a superposition principle for the fast ellipse fitting is developed to accelerate the process. Then, the ellipse candidates can be formulated by the hierarchical clustering of 5D parameter space of initial ellipse set. Finally, the salient ellipse candidates are selected as detections subject to the stringent and effective verification. Extensive experiments on three public datasets are implemented and our method achieves the best F-measure scores compared to the state-of-the-art methods.