High-Dimensional Private Empirical Risk Minimization by Greedy Coordinate Descent
Paper and Code
Jul 04, 2022
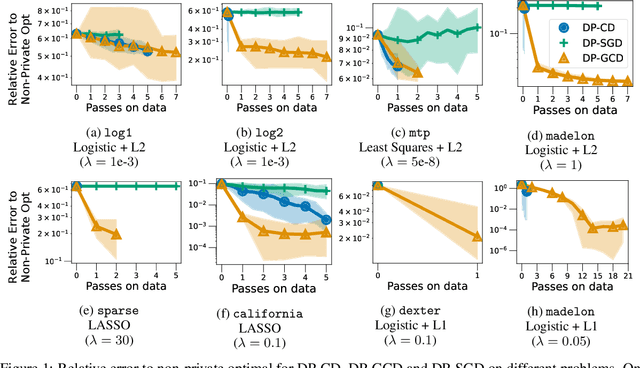
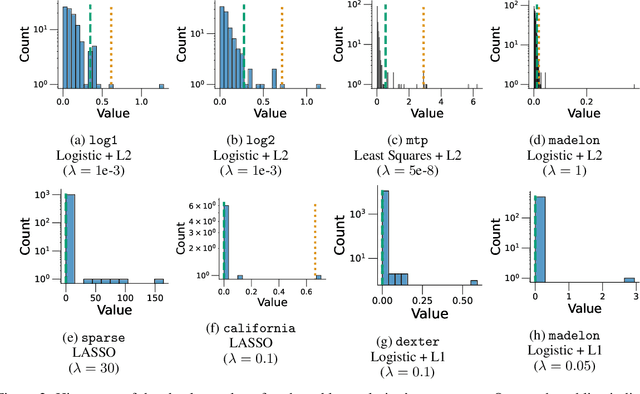
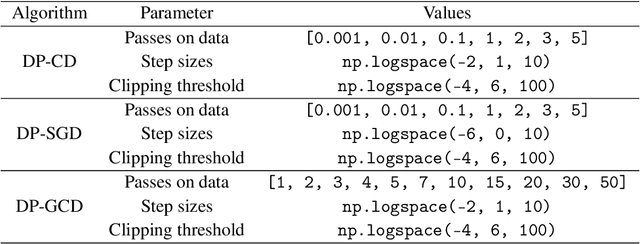
In this paper, we study differentially private empirical risk minimization (DP-ERM). It has been shown that the (worst-case) utility of DP-ERM reduces as the dimension increases. This is a major obstacle to privately learning large machine learning models. In high dimension, it is common for some model's parameters to carry more information than others. To exploit this, we propose a differentially private greedy coordinate descent (DP-GCD) algorithm. At each iteration, DP-GCD privately performs a coordinate-wise gradient step along the gradients' (approximately) greatest entry. We show theoretically that DP-GCD can improve utility by exploiting structural properties of the problem's solution (such as sparsity or quasi-sparsity), with very fast progress in early iterations. We then illustrate this numerically, both on synthetic and real datasets. Finally, we describe promising directions for future work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge