Hierarchical Width-Based Planning and Learning
Paper and Code
Jan 15, 2021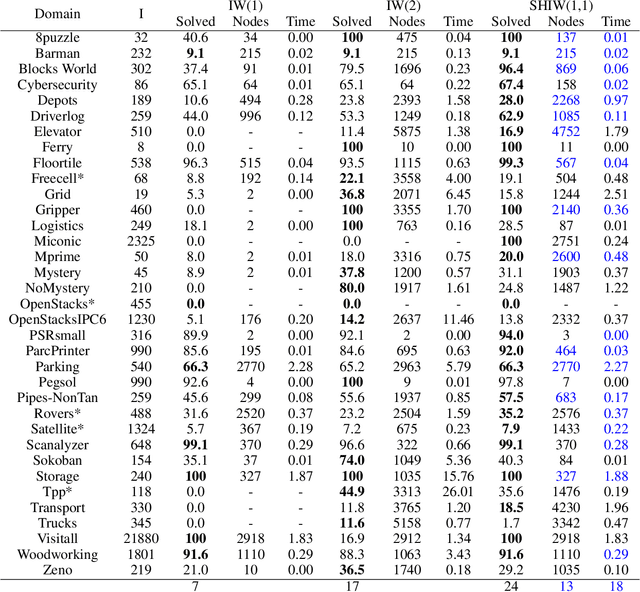
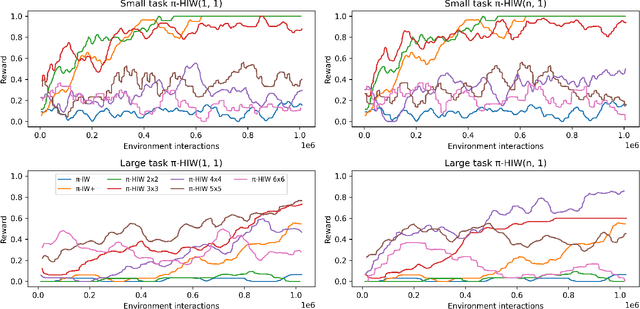
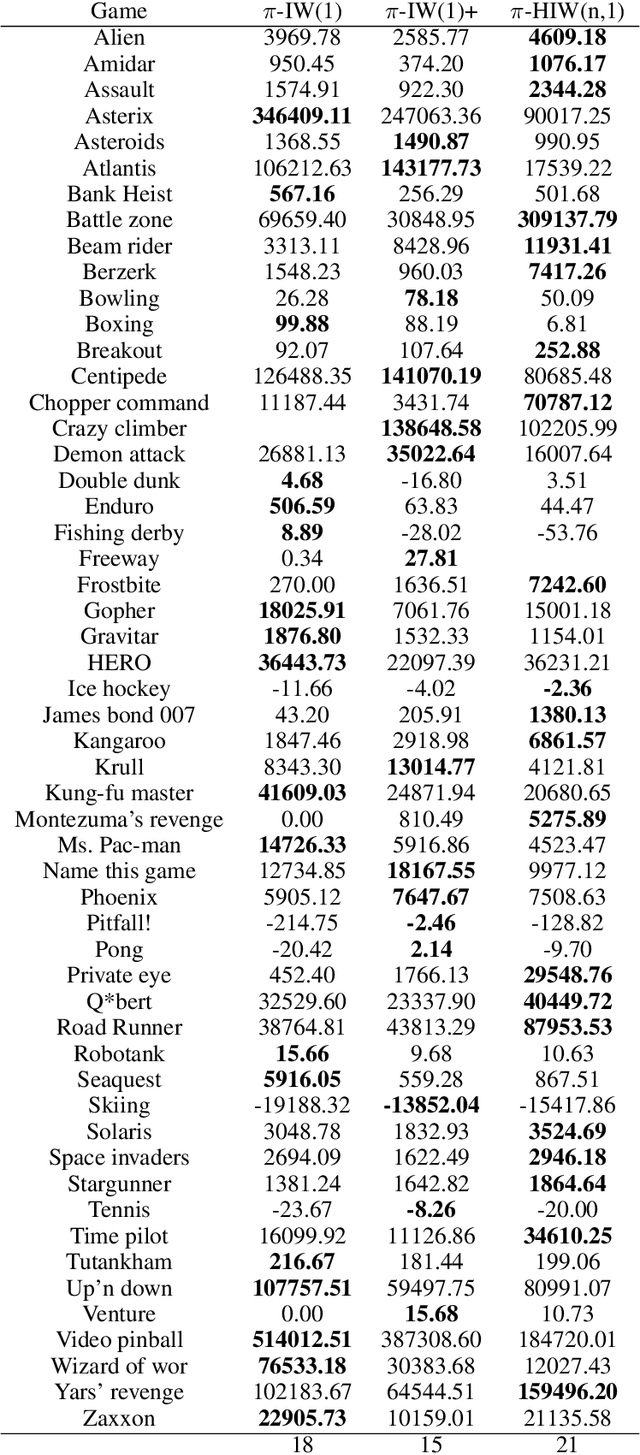
Width-based search methods have demonstrated state-of-the-art performance in a wide range of testbeds, from classical planning problems to image-based simulators such as Atari games. These methods scale independently of the size of the state-space, but exponentially in the problem width. In practice, running the algorithm with a width larger than 1 is computationally intractable, prohibiting IW from solving higher width problems. In this paper, we present a hierarchical algorithm that plans at two levels of abstraction. A high-level planner uses abstract features that are incrementally discovered from low-level pruning decisions. We illustrate this algorithm in classical planning PDDL domains as well as in pixel-based simulator domains. In classical planning, we show how IW(1) at two levels of abstraction can solve problems of width 2. For pixel-based domains, we show how in combination with a learned policy and a learned value function, the proposed hierarchical IW can outperform current flat IW-based planners in Atari games with sparse rewards.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge