Hierarchical Average Reward Policy Gradient Algorithms
Paper and Code
Nov 20, 2019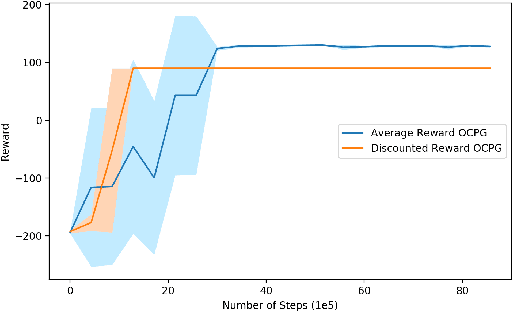

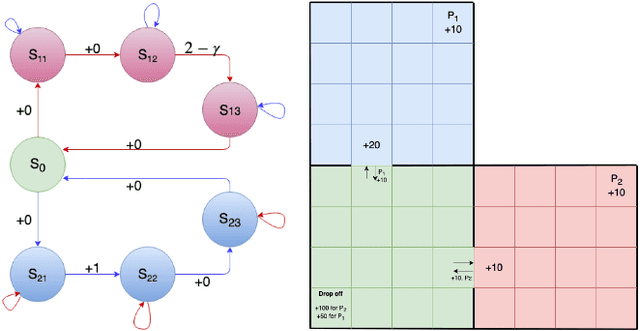
Option-critic learning is a general-purpose reinforcement learning (RL) framework that aims to address the issue of long term credit assignment by leveraging temporal abstractions. However, when dealing with extended timescales, discounting future rewards can lead to incorrect credit assignments. In this work, we address this issue by extending the hierarchical option-critic policy gradient theorem for the average reward criterion. Our proposed framework aims to maximize the long-term reward obtained in the steady-state of the Markov chain defined by the agent's policy. Furthermore, we use an ordinary differential equation based approach for our convergence analysis and prove that the parameters of the intra-option policies, termination functions, and value functions, converge to their corresponding optimal values, with probability one. Finally, we illustrate the competitive advantage of learning options, in the average reward setting, on a grid-world environment with sparse rewards.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge