Heavy-Tailed Regularization of Weight Matrices in Deep Neural Networks
Paper and Code
Apr 07, 2023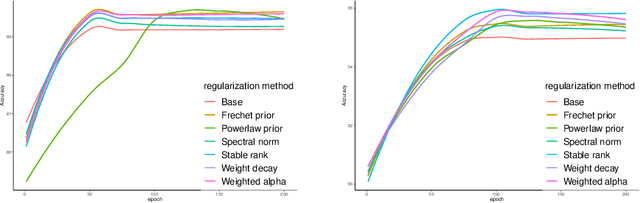
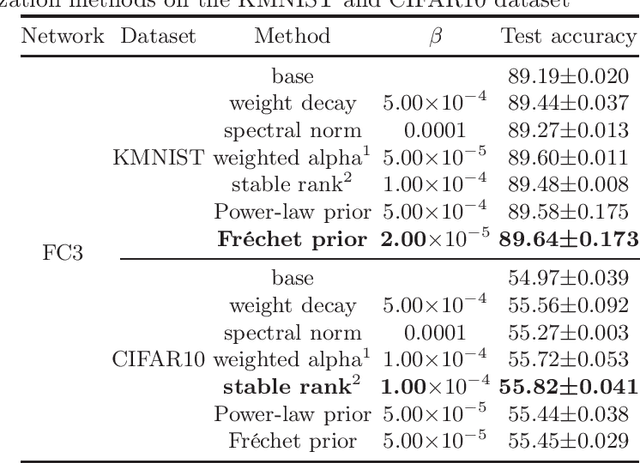

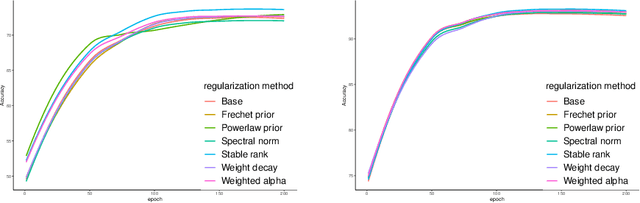
Unraveling the reasons behind the remarkable success and exceptional generalization capabilities of deep neural networks presents a formidable challenge. Recent insights from random matrix theory, specifically those concerning the spectral analysis of weight matrices in deep neural networks, offer valuable clues to address this issue. A key finding indicates that the generalization performance of a neural network is associated with the degree of heavy tails in the spectrum of its weight matrices. To capitalize on this discovery, we introduce a novel regularization technique, termed Heavy-Tailed Regularization, which explicitly promotes a more heavy-tailed spectrum in the weight matrix through regularization. Firstly, we employ the Weighted Alpha and Stable Rank as penalty terms, both of which are differentiable, enabling the direct calculation of their gradients. To circumvent over-regularization, we introduce two variations of the penalty function. Then, adopting a Bayesian statistics perspective and leveraging knowledge from random matrices, we develop two novel heavy-tailed regularization methods, utilizing Powerlaw distribution and Frechet distribution as priors for the global spectrum and maximum eigenvalues, respectively. We empirically show that heavytailed regularization outperforms conventional regularization techniques in terms of generalization performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge