HD-cos Networks: Efficient Neural Architectures for Secure Multi-Party Computation
Paper and Code
Oct 28, 2021
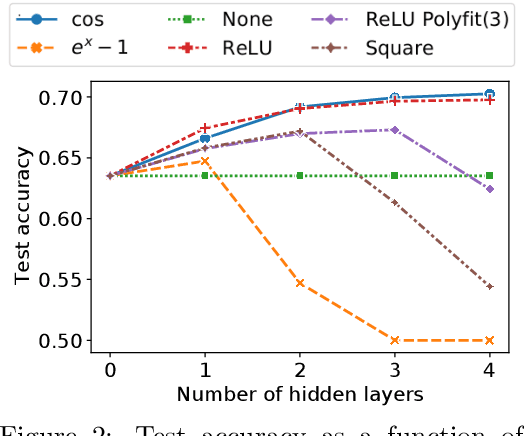
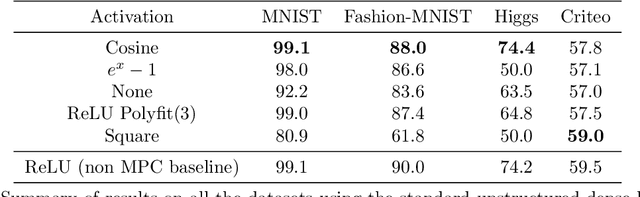

Multi-party computation (MPC) is a branch of cryptography where multiple non-colluding parties execute a well designed protocol to securely compute a function. With the non-colluding party assumption, MPC has a cryptographic guarantee that the parties will not learn sensitive information from the computation process, making it an appealing framework for applications that involve privacy-sensitive user data. In this paper, we study training and inference of neural networks under the MPC setup. This is challenging because the elementary operations of neural networks such as the ReLU activation function and matrix-vector multiplications are very expensive to compute due to the added multi-party communication overhead. To address this, we propose the HD-cos network that uses 1) cosine as activation function, 2) the Hadamard-Diagonal transformation to replace the unstructured linear transformations. We show that both of the approaches enjoy strong theoretical motivations and efficient computation under the MPC setup. We demonstrate on multiple public datasets that HD-cos matches the quality of the more expensive baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge