Group Fairness in Bandit Arm Selection

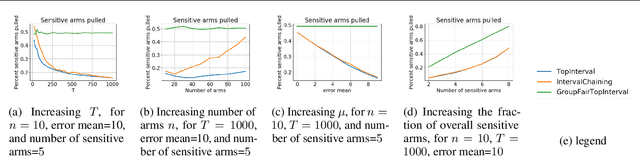
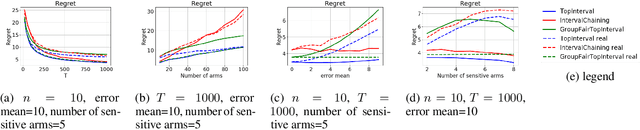
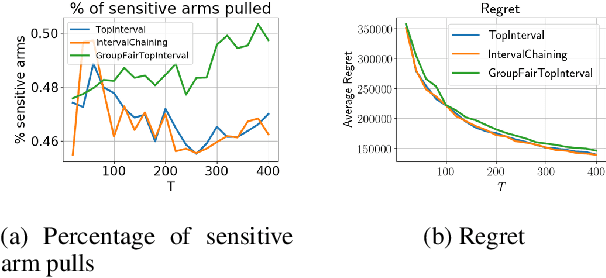
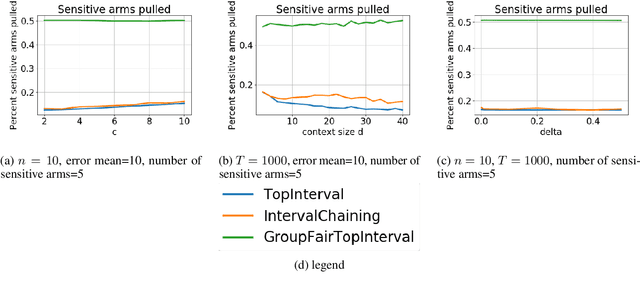
We consider group fairness in the contextual bandit setting. Here, a sequential decision maker must choose at each time step an arm to pull from a finite set of arms, after observing some context for each of the potential arm pulls. Additionally, arms are partitioned into m sensitive groups based on some protected feature (e.g., age, race, or socio-economic status). Despite the fact that there may be differences in expected payout between the groups, we may wish to ensure some form of fairness between picking arms from the various groups. In this work, we explore two definitions of fairness: equal group probability, wherein the probability of pulling an arm from any of the protected groups is the same; and proportional parity, wherein the probability of choosing an arm from a particular group is proportional to the size of that group. We provide a novel algorithm that can accommodate these notions of fairness and provide bounds on the regret for our algorithm. We test our algorithms on a hypothetical intervention setting wherein we want to allocate resources across protected groups.