Greed is Good: Near-Optimal Submodular Maximization via Greedy Optimization
Paper and Code
Apr 05, 2017
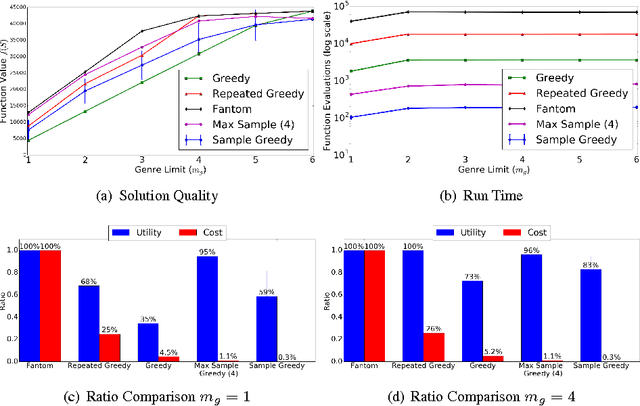

It is known that greedy methods perform well for maximizing monotone submodular functions. At the same time, such methods perform poorly in the face of non-monotonicity. In this paper, we show - arguably, surprisingly - that invoking the classical greedy algorithm $O(\sqrt{k})$-times leads to the (currently) fastest deterministic algorithm, called Repeated Greedy, for maximizing a general submodular function subject to $k$-independent system constraints. Repeated Greedy achieves $(1 + O(1/\sqrt{k}))k$ approximation using $O(nr\sqrt{k})$ function evaluations (here, $n$ and $r$ denote the size of the ground set and the maximum size of a feasible solution, respectively). We then show that by a careful sampling procedure, we can run the greedy algorithm only once and obtain the (currently) fastest randomized algorithm, called Sample Greedy, for maximizing a submodular function subject to $k$-extendible system constraints (a subclass of $k$-independent system constrains). Sample Greedy achieves $(k + 3)$-approximation with only $O(nr/k)$ function evaluations. Finally, we derive an almost matching lower bound, and show that no polynomial time algorithm can have an approximation ratio smaller than $ k + 1/2 - \varepsilon$. To further support our theoretical results, we compare the performance of Repeated Greedy and Sample Greedy with prior art in a concrete application (movie recommendation). We consistently observe that while Sample Greedy achieves practically the same utility as the best baseline, it performs at least two orders of magnitude faster.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge