Graph Regularized Tensor Sparse Coding for Image Representation
Paper and Code
Mar 27, 2017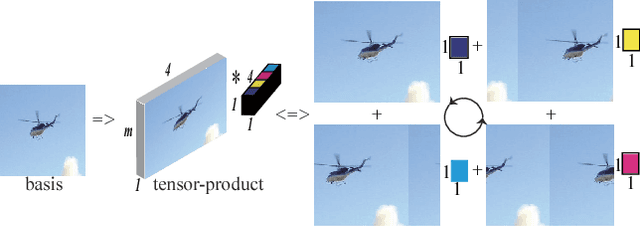
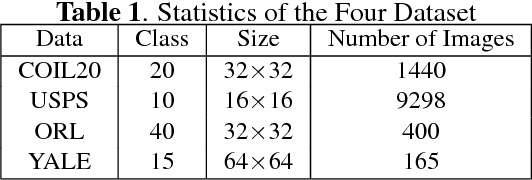
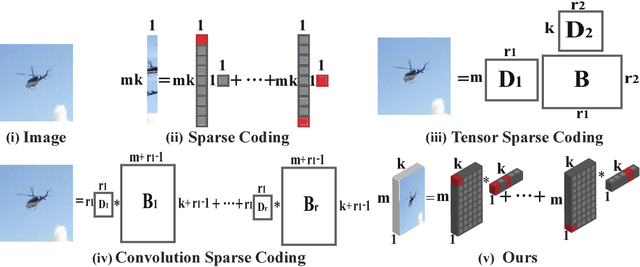
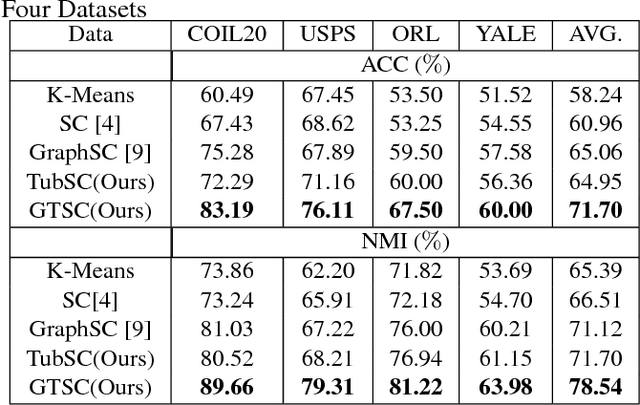
Sparse coding (SC) is an unsupervised learning scheme that has received an increasing amount of interests in recent years. However, conventional SC vectorizes the input images, which destructs the intrinsic spatial structures of the images. In this paper, we propose a novel graph regularized tensor sparse coding (GTSC) for image representation. GTSC preserves the local proximity of elementary structures in the image by adopting the newly proposed tubal-tensor representation. Simultaneously, it considers the intrinsic geometric properties by imposing graph regularization that has been successfully applied to uncover the geometric distribution for the image data. Moreover, the returned sparse representations by GTSC have better physical explanations as the key operation (i.e., circular convolution) in the tubal-tensor model preserves the shifting invariance property. Experimental results on image clustering demonstrate the effectiveness of the proposed scheme.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge