Graph Neural Networks with Feature and Structure Aware Random Walk
Paper and Code
Nov 19, 2021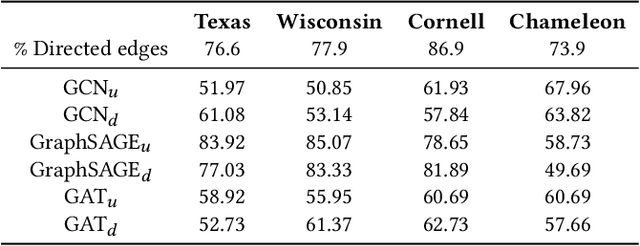
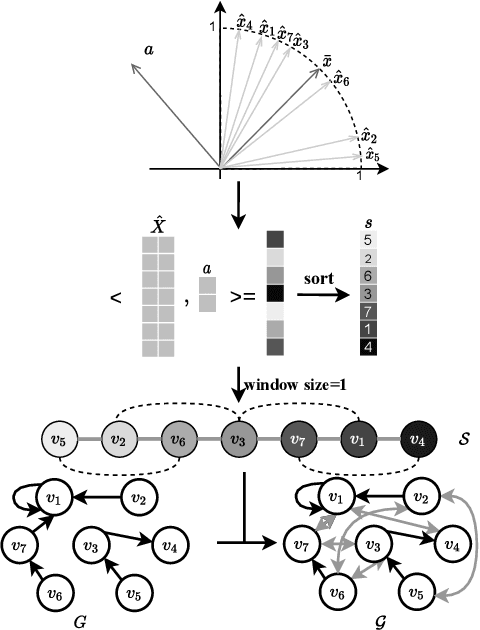
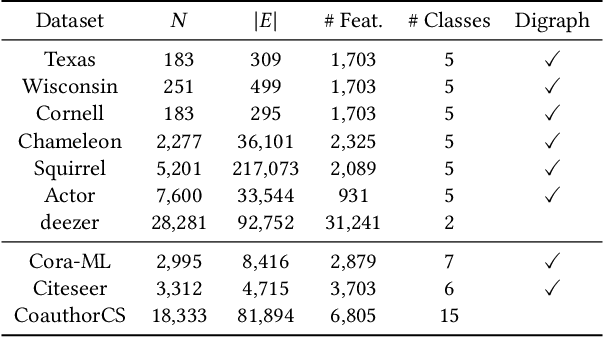
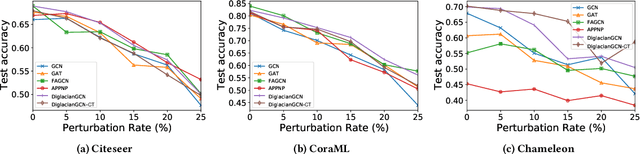
Graph Neural Networks (GNNs) have received increasing attention for representation learning in various machine learning tasks. However, most existing GNNs applying neighborhood aggregation usually perform poorly on the graph with heterophily where adjacent nodes belong to different classes. In this paper, we show that in typical heterphilous graphs, the edges may be directed, and whether to treat the edges as is or simply make them undirected greatly affects the performance of the GNN models. Furthermore, due to the limitation of heterophily, it is highly beneficial for the nodes to aggregate messages from similar nodes beyond local neighborhood.These motivate us to develop a model that adaptively learns the directionality of the graph, and exploits the underlying long-distance correlations between nodes. We first generalize the graph Laplacian to digraph based on the proposed Feature-Aware PageRank algorithm, which simultaneously considers the graph directionality and long-distance feature similarity between nodes. Then digraph Laplacian defines a graph propagation matrix that leads to a model called {\em DiglacianGCN}. Based on this, we further leverage the node proximity measured by commute times between nodes, in order to preserve the nodes' long-distance correlation on the topology level. Extensive experiments on ten datasets with different levels of homophily demonstrate the effectiveness of our method over existing solutions in the task of node classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge