Gradient tree boosting with random output projections for multi-label classification and multi-output regression
Paper and Code
May 18, 2019
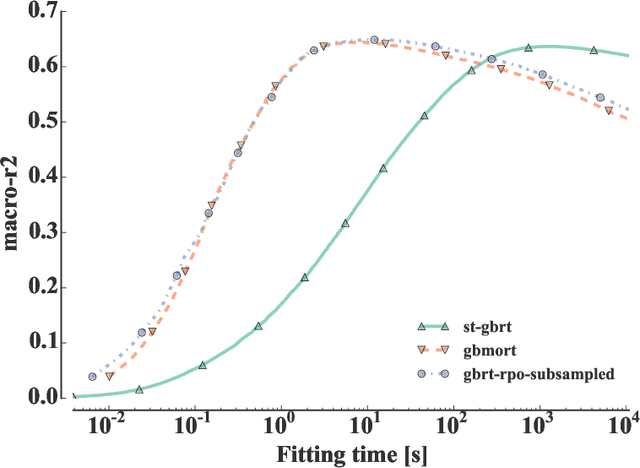
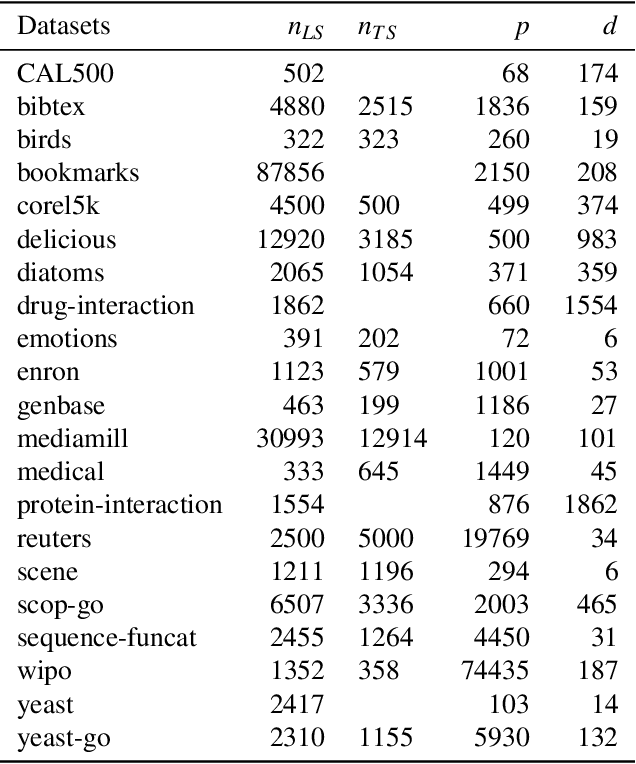
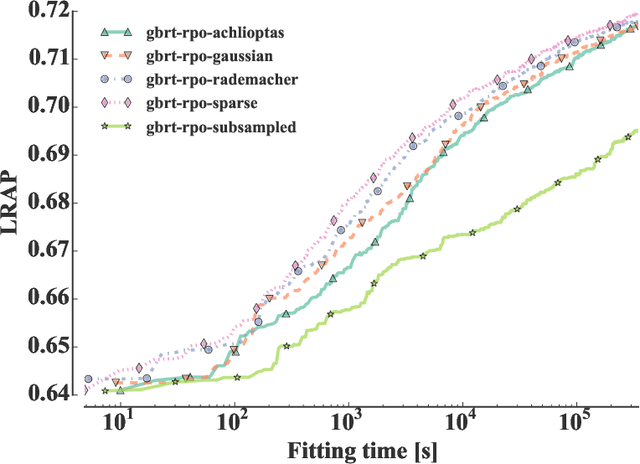
In many applications of supervised learning, multiple classification or regression outputs have to be predicted jointly. We consider several extensions of gradient boosting to address such problems. We first propose a straightforward adaptation of gradient boosting exploiting multiple output regression trees as base learners. We then argue that this method is only expected to be optimal when the outputs are fully correlated, as it forces the partitioning induced by the tree base learners to be shared by all outputs. We then propose a novel extension of gradient tree boosting to specifically address this issue. At each iteration of this new method, a regression tree structure is grown to fit a single random projection of the current residuals and the predictions of this tree are fitted linearly to the current residuals of all the outputs, independently. Because of this linear fit, the method can adapt automatically to any output correlation structure. Extensive experiments are conducted with this method, as well as other algorithmic variants, on several artificial and real problems. Randomly projecting the output space is shown to provide a better adaptation to different output correlation patterns and is therefore competitive with the best of the other methods in most settings. Thanks to model sharing, the convergence speed is also improved, reducing the computing times (or the complexity of the model) to reach a specific accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge