Gradient-Coherent Strong Regularization for Deep Neural Networks

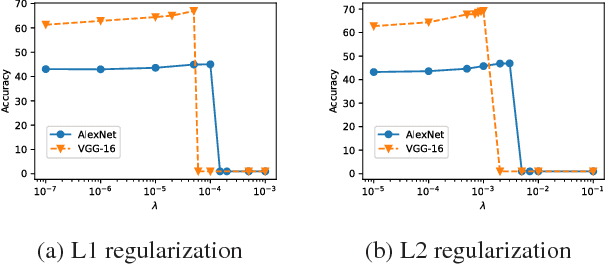
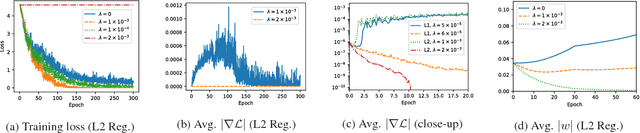
Deep neural networks are often prone to over-fitting with their numerous parameters, so regularization plays an important role in generalization. L1 and L2 regularizers are common regularization tools in machine learning with their simplicity and effectiveness. However, we observe that imposing strong L1 or L2 regularization on deep neural networks with stochastic gradient descent easily fails, which limits the generalization ability of the underlying neural networks. To understand this phenomenon, we first investigate how and why learning fails when strong regularization is imposed on deep neural networks. We then propose a novel method, gradient-coherent strong regularization, which imposes regularization only when the gradients are kept coherent in the presence of strong regularization. Experiments are performed with multiple deep architectures on three benchmark data sets for image recognition. Experimental results show that our proposed approach indeed endures strong regularization and significantly improves both accuracy and compression, which could not be achieved otherwise.