Gradient-based Competitive Learning: Theory
Paper and Code
Sep 06, 2020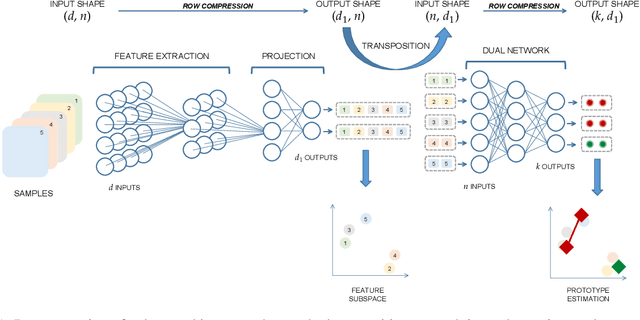
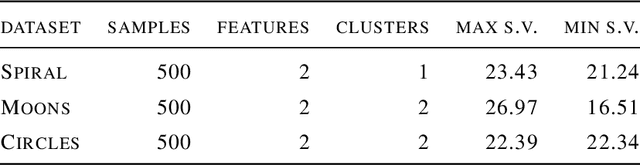
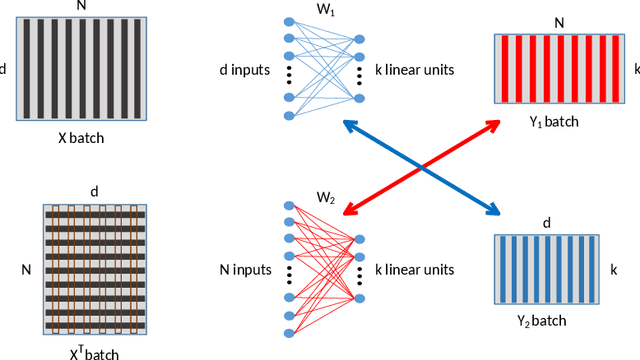
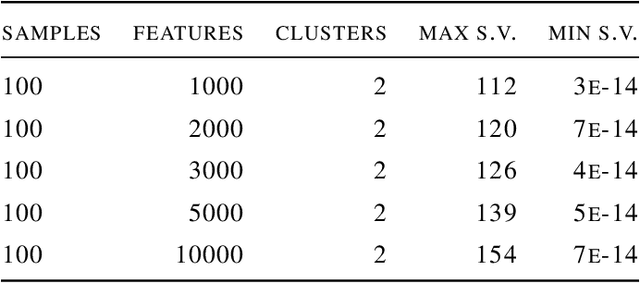
Deep learning has been widely used for supervised learning and classification/regression problems. Recently, a novel area of research has applied this paradigm to unsupervised tasks; indeed, a gradient-based approach extracts, efficiently and autonomously, the relevant features for handling input data. However, state-of-the-art techniques focus mostly on algorithmic efficiency and accuracy rather than mimic the input manifold. On the contrary, competitive learning is a powerful tool for replicating the input distribution topology. This paper introduces a novel perspective in this area by combining these two techniques: unsupervised gradient-based and competitive learning. The theory is based on the intuition that neural networks are able to learn topological structures by working directly on the transpose of the input matrix. At this purpose, the vanilla competitive layer and its dual are presented. The former is just an adaptation of a standard competitive layer for deep clustering, while the latter is trained on the transposed matrix. Their equivalence is extensively proven both theoretically and experimentally. However, the dual layer is better suited for handling very high-dimensional datasets. The proposed approach has a great potential as it can be generalized to a vast selection of topological learning tasks, such as non-stationary and hierarchical clustering; furthermore, it can also be integrated within more complex architectures such as autoencoders and generative adversarial networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge