Gradient Agreement as an Optimization Objective for Meta-Learning
Paper and Code
Oct 18, 2018
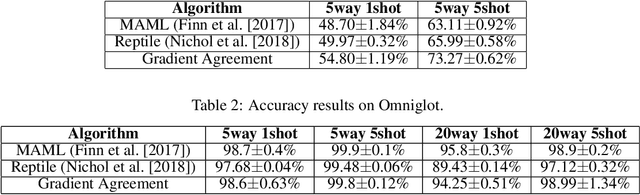
This paper presents a novel optimization method for maximizing generalization over tasks in meta-learning. The goal of meta-learning is to learn a model for an agent adapting rapidly when presented with previously unseen tasks. Tasks are sampled from a specific distribution which is assumed to be similar for both seen and unseen tasks. We focus on a family of meta-learning methods learning initial parameters of a base model which can be fine-tuned quickly on a new task, by few gradient steps (MAML). Our approach is based on pushing the parameters of the model to a direction in which tasks have more agreement upon. If the gradients of a task agree with the parameters update vector, then their inner product will be a large positive value. As a result, given a batch of tasks to be optimized for, we associate a positive (negative) weight to the loss function of a task, if the inner product between its gradients and the average of the gradients of all tasks in the batch is a positive (negative) value. Therefore, the degree of the contribution of a task to the parameter updates is controlled by introducing a set of weights on the loss function of the tasks. Our method can be easily integrated with the current meta-learning algorithms for neural networks. Our experiments demonstrate that it yields models with better generalization compared to MAML and Reptile.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge