GM-VAE: Representation Learning with VAE on Gaussian Manifold
Paper and Code
Sep 30, 2022

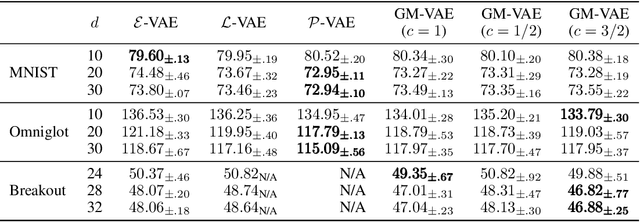

We propose a Gaussian manifold variational auto-encoder (GM-VAE) whose latent space consists of a set of diagonal Gaussian distributions. It is known that the set of the diagonal Gaussian distributions with the Fisher information metric forms a product hyperbolic space, which we call a Gaussian manifold. To learn the VAE endowed with the Gaussian manifold, we first propose a pseudo Gaussian manifold normal distribution based on the Kullback-Leibler divergence, a local approximation of the squared Fisher-Rao distance, to define a density over the latent space. With the newly proposed distribution, we introduce geometric transformations at the last and the first of the encoder and the decoder of VAE, respectively to help the transition between the Euclidean and Gaussian manifolds. Through the empirical experiments, we show competitive generalization performance of GM-VAE against other variants of hyperbolic- and Euclidean-VAEs. Our model achieves strong numerical stability, which is a common limitation reported with previous hyperbolic-VAEs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge