Globally optimal registration of noisy point clouds
Paper and Code
Aug 22, 2019
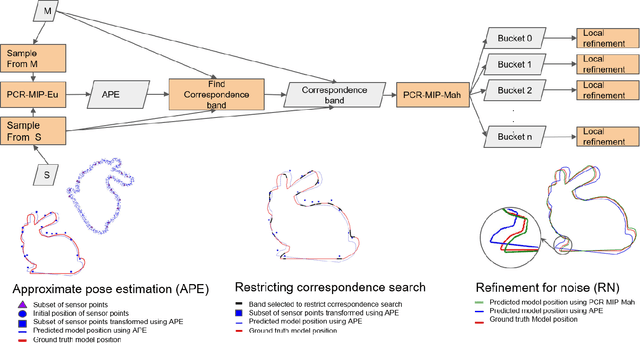
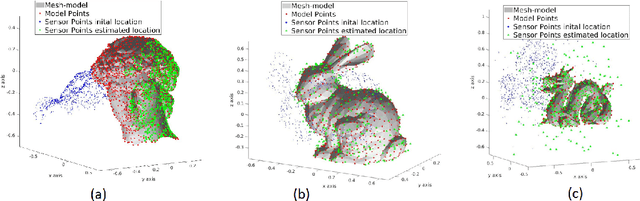

Registration of 3D point clouds is a fundamental task in several applications of robotics and computer vision. While registration methods such as iterative closest point and variants are very popular, they are only locally optimal. There has been some recent work on globally optimal registration, but they perform poorly in the presence of noise in the measurements. In this work we develop a mixed integer programming-based approach for globally optimal registration that explicitly considers uncertainty in its optimization, and hence produces more accurate estimates. Furthermore, from a practical implementation perspective we develop a multi-step optimization that combines fast local methods with our accurate global formulation. Through extensive simulation and real world experiments we demonstrate improved performance over state-of-the-art methods for various level of noise and outliers in the data as well as for partial geometric overlap.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge