Geometry-Consistent Adversarial Networks for One-Sided Unsupervised Domain Mapping

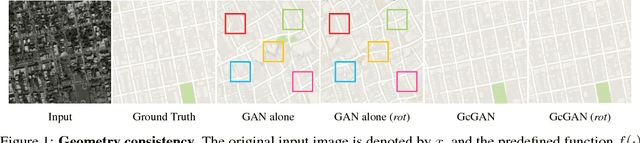
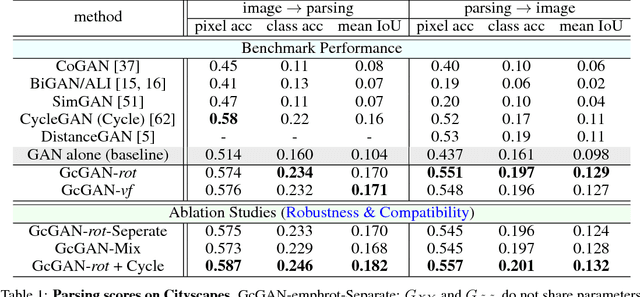
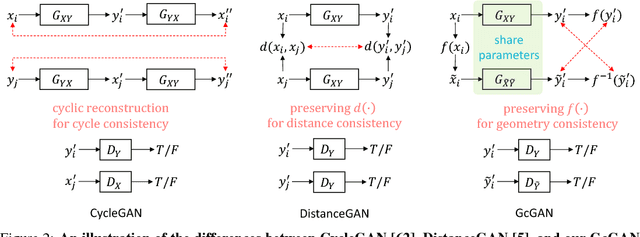
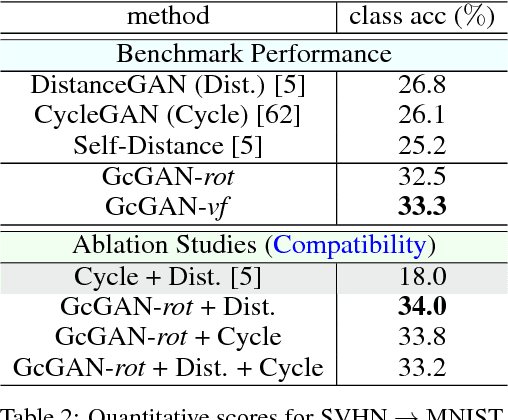
Unsupervised domain mapping aims at learning a function to translate domain X to Y (GXY : X to Y) in the absence of paired (X,Y) samples. Finding the optimal GXY without paired data is an ill-posed problem and hence appropriate constraints are required to obtain reasonable solutions. One of the most prominent constraint is cycle-consistency, which enforces the translated image by GXY to be translated back to the input image by an inverse mapping GYX. While cycle-consistency requires simultaneous training of GXY and GYX, recent methods have demonstrated one-sided domain mapping (only learn GXY) can be achieved by preserving pairwise distance between images before and after translation. Although cycle-consistency and distance preserving successfully constrain the solution space, they overlook the special properties of images that simple geometric transformations do not change the semantics of an image. Based on this special property, we develop a geometry-consistent adversarial network (GcGAN) which enables one-sided unsupervised domain mapping. Our GcGAN takes the original image and its counterpart image transformed by a predefined geometric transformation as inputs and generates two images in the new domain with the corresponding geometry-consistency constraint. The geometry-consistency constraint eliminates unreasonable solutions and produce more reliable solutions. Quantitative comparisons against baseline (GAN alone) and the state-of-the-art methods, including DistanceGAN and CycleGAN, demonstrate the superiority of our method in generating realistic images.