Geometry and Expressive Power of Conditional Restricted Boltzmann Machines
Paper and Code
Mar 12, 2015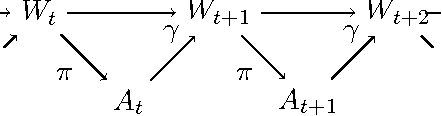
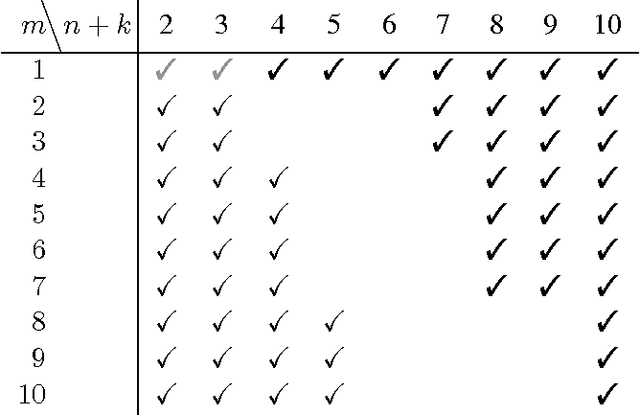
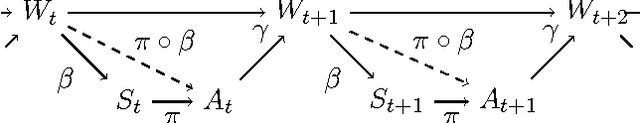
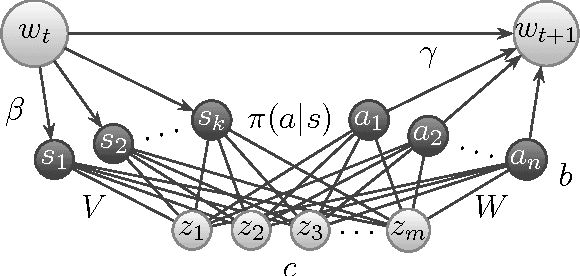
Conditional restricted Boltzmann machines are undirected stochastic neural networks with a layer of input and output units connected bipartitely to a layer of hidden units. These networks define models of conditional probability distributions on the states of the output units given the states of the input units, parametrized by interaction weights and biases. We address the representational power of these models, proving results their ability to represent conditional Markov random fields and conditional distributions with restricted supports, the minimal size of universal approximators, the maximal model approximation errors, and on the dimension of the set of representable conditional distributions. We contribute new tools for investigating conditional probability models, which allow us to improve the results that can be derived from existing work on restricted Boltzmann machine probability models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge