Geometry and Determinism of Optimal Stationary Control in Partially Observable Markov Decision Processes
Paper and Code
Feb 13, 2016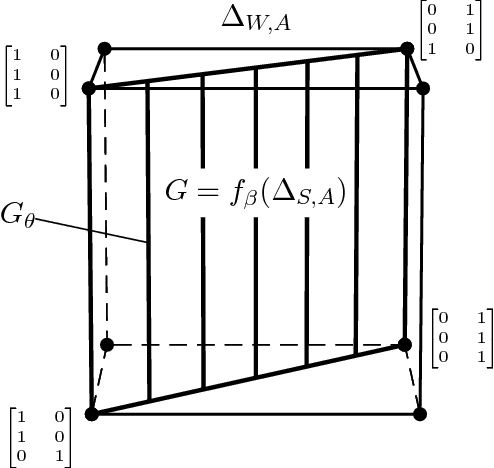
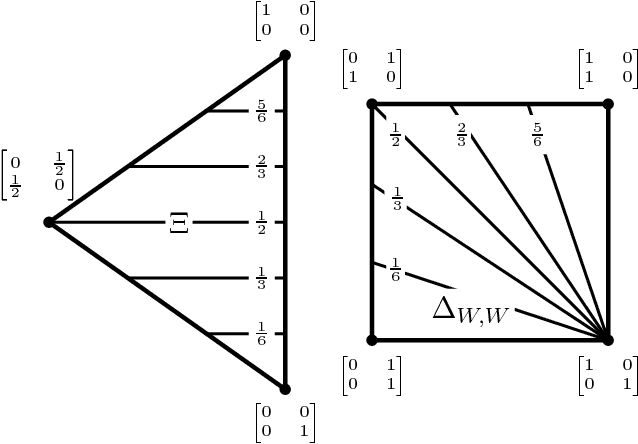
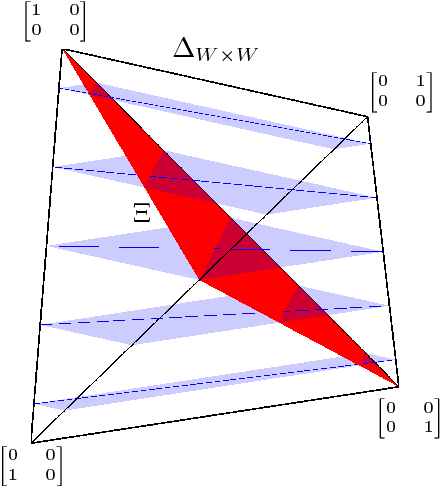
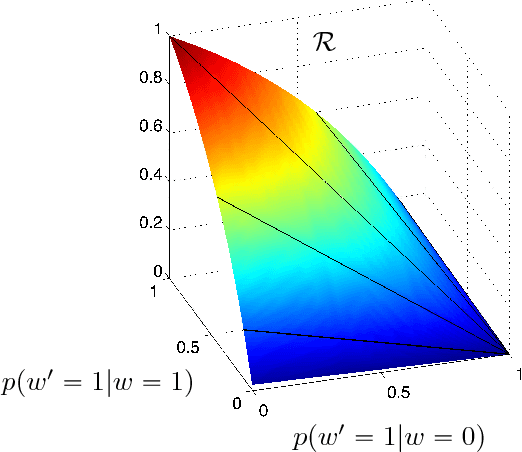
It is well known that for any finite state Markov decision process (MDP) there is a memoryless deterministic policy that maximizes the expected reward. For partially observable Markov decision processes (POMDPs), optimal memoryless policies are generally stochastic. We study the expected reward optimization problem over the set of memoryless stochastic policies. We formulate this as a constrained linear optimization problem and develop a corresponding geometric framework. We show that any POMDP has an optimal memoryless policy of limited stochasticity, which allows us to reduce the dimensionality of the search space. Experiments demonstrate that this approach enables better and faster convergence of the policy gradient on the evaluated systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge