Geometric Enclosing Networks
Paper and Code
Aug 17, 2017


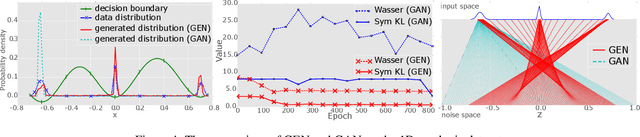
Training model to generate data has increasingly attracted research attention and become important in modern world applications. We propose in this paper a new geometry-based optimization approach to address this problem. Orthogonal to current state-of-the-art density-based approaches, most notably VAE and GAN, we present a fresh new idea that borrows the principle of minimal enclosing ball to train a generator G\left(\bz\right) in such a way that both training and generated data, after being mapped to the feature space, are enclosed in the same sphere. We develop theory to guarantee that the mapping is bijective so that its inverse from feature space to data space results in expressive nonlinear contours to describe the data manifold, hence ensuring data generated are also lying on the data manifold learned from training data. Our model enjoys a nice geometric interpretation, hence termed Geometric Enclosing Networks (GEN), and possesses some key advantages over its rivals, namely simple and easy-to-control optimization formulation, avoidance of mode collapsing and efficiently learn data manifold representation in a completely unsupervised manner. We conducted extensive experiments on synthesis and real-world datasets to illustrate the behaviors, strength and weakness of our proposed GEN, in particular its ability to handle multi-modal data and quality of generated data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge