Geometric algorithms for predicting resilience and recovering damage in neural networks
Paper and Code
Jun 02, 2020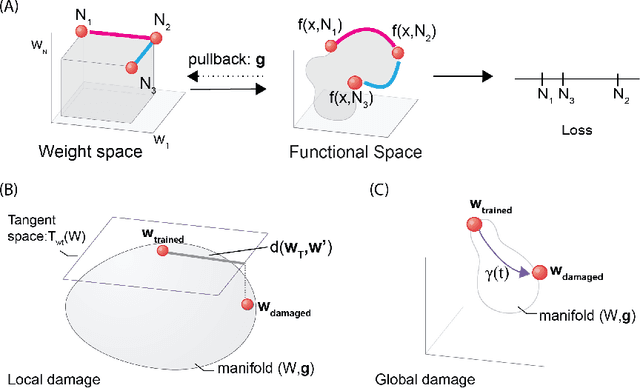
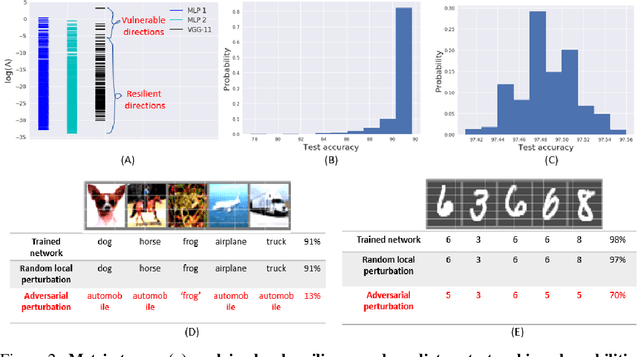
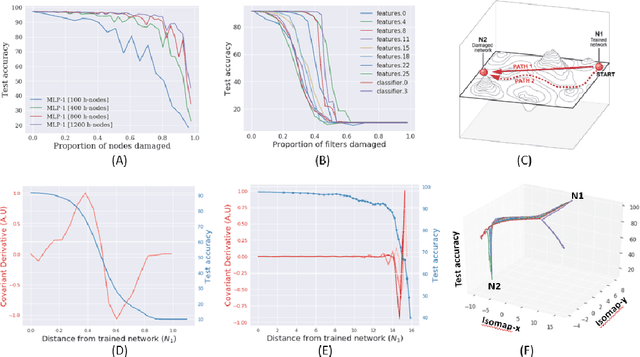
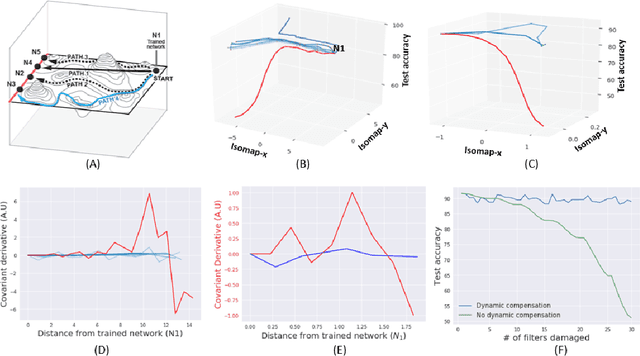
Biological neural networks have evolved to maintain performance despite significant circuit damage. To survive damage, biological network architectures have both intrinsic resilience to component loss and also activate recovery programs that adjust network weights through plasticity to stabilize performance. Despite the importance of resilience in technology applications, the resilience of artificial neural networks is poorly understood, and autonomous recovery algorithms have yet to be developed. In this paper, we establish a mathematical framework to analyze the resilience of artificial neural networks through the lens of differential geometry. Our geometric language provides natural algorithms that identify local vulnerabilities in trained networks as well as recovery algorithms that dynamically adjust networks to compensate for damage. We reveal striking vulnerabilities in commonly used image analysis networks, like MLP's and CNN's trained on MNIST and CIFAR10 respectively. We also uncover high-performance recovery paths that enable the same networks to dynamically re-adjust their parameters to compensate for damage. Broadly, our work provides procedures that endow artificial systems with resilience and rapid-recovery routines to enhance their integration with IoT devices as well as enable their deployment for critical applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge