Genetic Programming for Manifold Learning: Preserving Local Topology
Paper and Code
Aug 23, 2021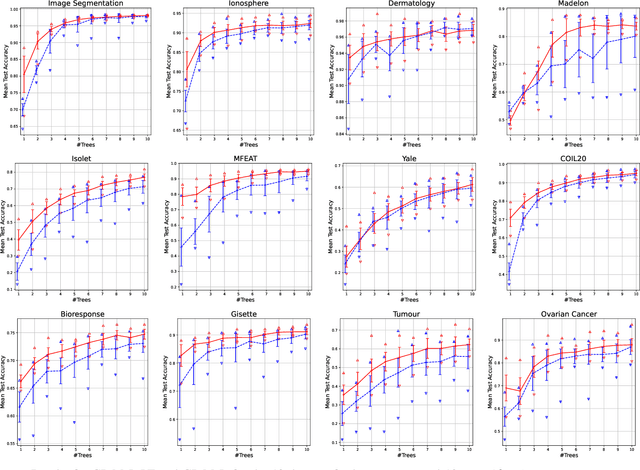

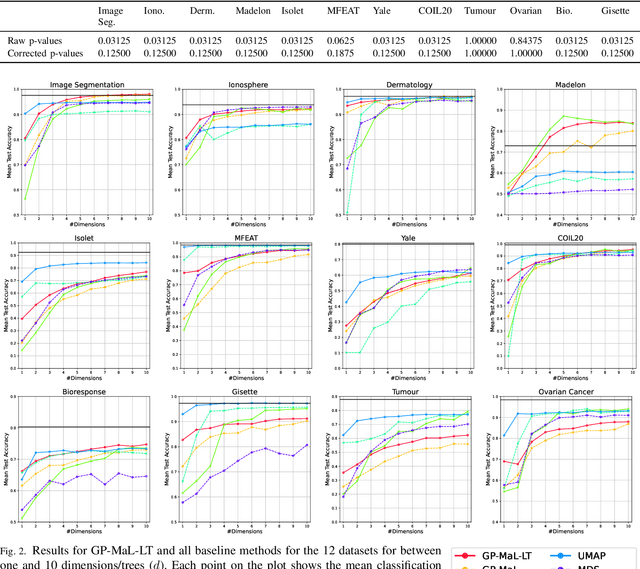
Manifold learning methods are an invaluable tool in today's world of increasingly huge datasets. Manifold learning algorithms can discover a much lower-dimensional representation (embedding) of a high-dimensional dataset through non-linear transformations that preserve the most important structure of the original data. State-of-the-art manifold learning methods directly optimise an embedding without mapping between the original space and the discovered embedded space. This makes interpretability - a key requirement in exploratory data analysis - nearly impossible. Recently, genetic programming has emerged as a very promising approach to manifold learning by evolving functional mappings from the original space to an embedding. However, genetic programming-based manifold learning has struggled to match the performance of other approaches. In this work, we propose a new approach to using genetic programming for manifold learning, which preserves local topology. This is expected to significantly improve performance on tasks where local neighbourhood structure (topology) is paramount. We compare our proposed approach with various baseline manifold learning methods and find that it often outperforms other methods, including a clear improvement over previous genetic programming approaches. These results are particularly promising, given the potential interpretability and reusability of the evolved mappings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge