General models for rational cameras and the case of two-slit projections
Paper and Code
Apr 11, 2017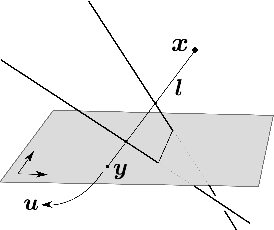
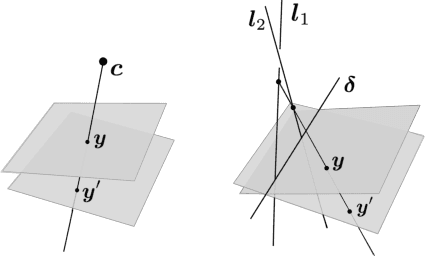
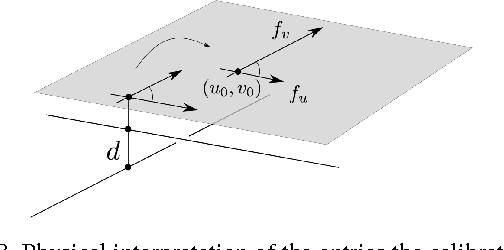
The rational camera model recently introduced in [19] provides a general methodology for studying abstract nonlinear imaging systems and their multi-view geometry. This paper builds on this framework to study "physical realizations" of rational cameras. More precisely, we give an explicit account of the mapping between between physical visual rays and image points (missing in the original description), which allows us to give simple analytical expressions for direct and inverse projections. We also consider "primitive" camera models, that are orbits under the action of various projective transformations, and lead to a general notion of intrinsic parameters. The methodology is general, but it is illustrated concretely by an in-depth study of two-slit cameras, that we model using pairs of linear projections. This simple analytical form allows us to describe models for the corresponding primitive cameras, to introduce intrinsic parameters with a clear geometric meaning, and to define an epipolar tensor characterizing two-view correspondences. In turn, this leads to new algorithms for structure from motion and self-calibration.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge