GEC-DePenD: Non-Autoregressive Grammatical Error Correction with Decoupled Permutation and Decoding
Paper and Code
Nov 14, 2023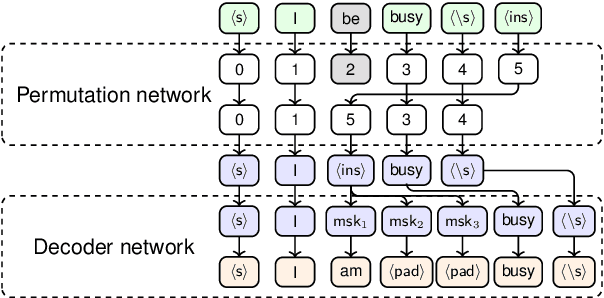
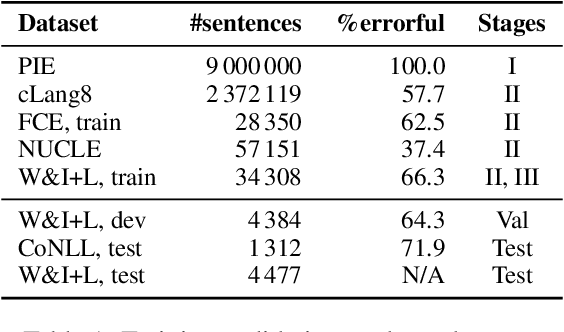
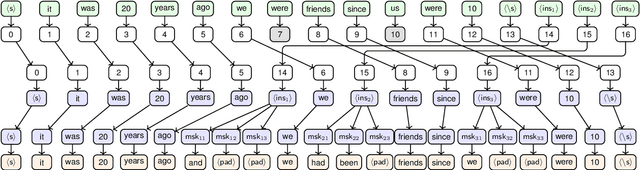
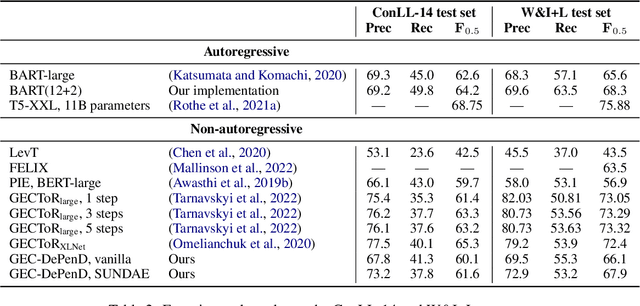
Grammatical error correction (GEC) is an important NLP task that is currently usually solved with autoregressive sequence-to-sequence models. However, approaches of this class are inherently slow due to one-by-one token generation, so non-autoregressive alternatives are needed. In this work, we propose a novel non-autoregressive approach to GEC that decouples the architecture into a permutation network that outputs a self-attention weight matrix that can be used in beam search to find the best permutation of input tokens (with auxiliary {ins} tokens) and a decoder network based on a step-unrolled denoising autoencoder that fills in specific tokens. This allows us to find the token permutation after only one forward pass of the permutation network, avoiding autoregressive constructions. We show that the resulting network improves over previously known non-autoregressive methods for GEC and reaches the level of autoregressive methods that do not use language-specific synthetic data generation methods. Our results are supported by a comprehensive experimental validation on the ConLL-2014 and Write&Improve+LOCNESS datasets and an extensive ablation study that supports our architectural and algorithmic choices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge