Gaussian Process Regression in Logarithmic Time
Paper and Code
Mar 10, 2021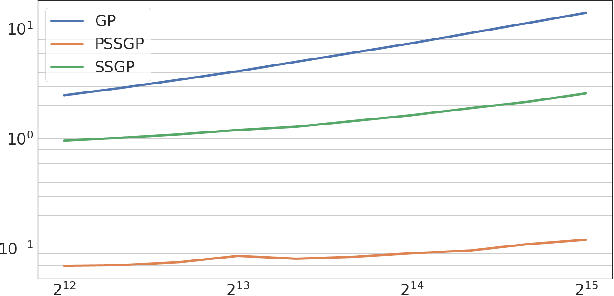
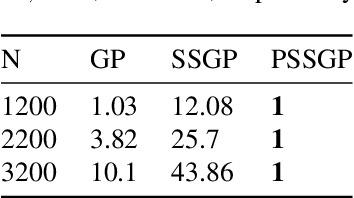
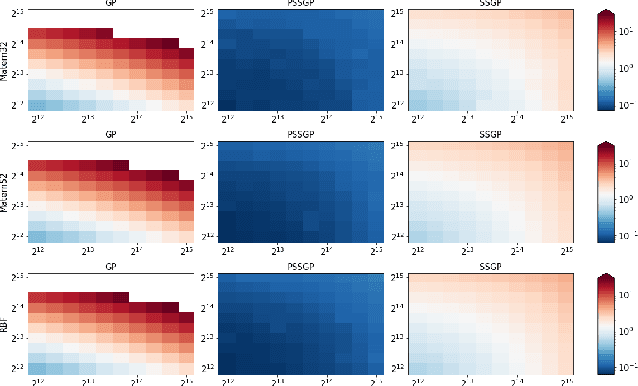
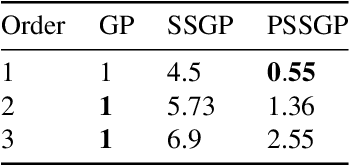
The aim of this article is to present a novel parallelization method for temporal Gaussian process (GP) regression problems. The method allows for solving GP regression problems in logarithmic $O(\log N)$ time, where $N$ is the number of time steps. Our approach uses the state-space representation of GPs which in its original form allows for linear $O(N)$ time GP regression by leveraging the Kalman filtering and smoothing methods. By using a recently proposed parallelization method for Bayesian filters and smoothers, we are able to reduce the linear computational complexity of the Kalman filter and smoother solutions to the GP regression problems into logarithmic span complexity, which transforms into logarithm time complexity when implemented in parallel hardware such as a graphics processing unit (GPU). We experimentally demonstrate the computational benefits one simulated and real datasets via our open-source implementation leveraging the GPflow framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge