GANs with Variational Entropy Regularizers: Applications in Mitigating the Mode-Collapse Issue
Paper and Code
Sep 24, 2020
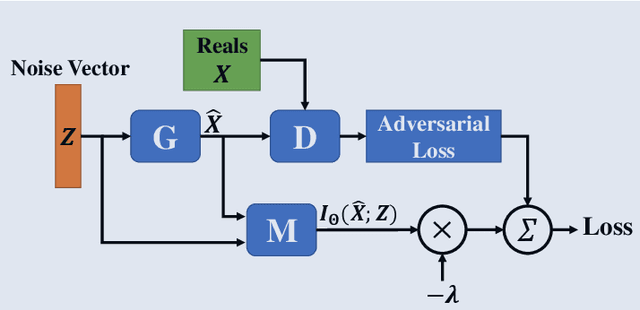
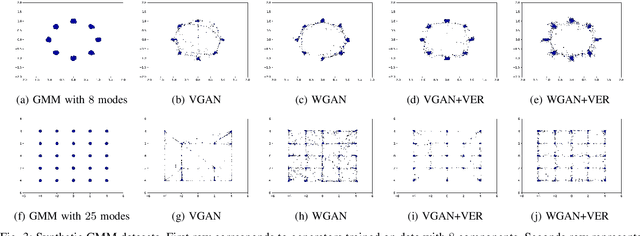
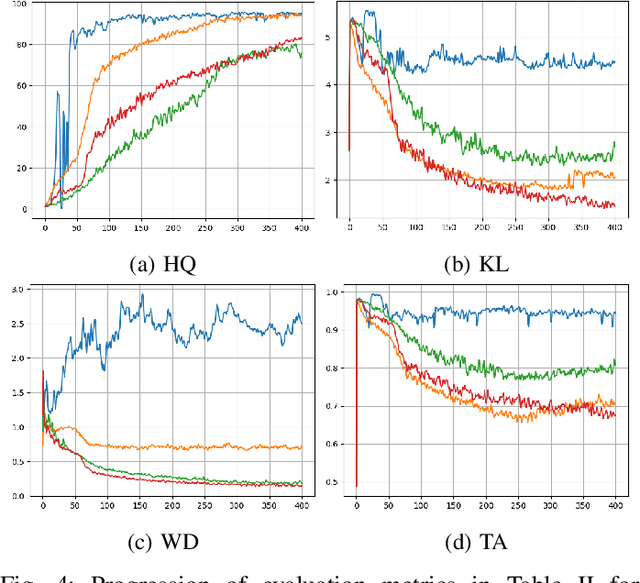
Building on the success of deep learning, Generative Adversarial Networks (GANs) provide a modern approach to learn a probability distribution from observed samples. GANs are often formulated as a zero-sum game between two sets of functions; the generator and the discriminator. Although GANs have shown great potentials in learning complex distributions such as images, they often suffer from the mode collapse issue where the generator fails to capture all existing modes of the input distribution. As a consequence, the diversity of generated samples is lower than that of the observed ones. To tackle this issue, we take an information-theoretic approach and maximize a variational lower bound on the entropy of the generated samples to increase their diversity. We call this approach GANs with Variational Entropy Regularizers (GAN+VER). Existing remedies for the mode collapse issue in GANs can be easily coupled with our proposed variational entropy regularization. Through extensive experimentation on standard benchmark datasets, we show all the existing evaluation metrics highlighting difference of real and generated samples are significantly improved with GAN+VER.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge